PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet us recall that if the sum of the two acute angles is \(90^{\circ}\), then the angles are said to be complementary.
In a right-angled triangle, the sum of two acute angles are \(90^{\circ}\).
That is, we can say that the two acute angles in a right-angled triangle are complementary.
Consider the triangle \(PQR\) right-angled at \(P\).
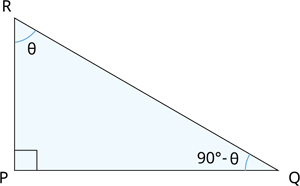
Here \(R\) and \(Q\) are complementary angles.
Therefore if \(\angle R\) \(=\) \(\theta\), then \(\angle Q\) \(=\) \(90^{\circ} - \theta\).
Let us write all the trigonometric ratios with respect to \(\angle R\) \(=\) \(\theta\) in a table.
Table \(1\):
Trigonometric ratio | Relationship with the \(\Delta PQR\) | Trigonometric ratio | Relationship with the \(\Delta PQR\) |
\(\sin \theta\) | \(\sin \theta\) \(=\) \(\frac{PQ}{RQ}\) | \(\text{cosec}\,\theta\) | \(\text{cosec}\,\theta\) \(=\) \(\frac{RQ}{PQ}\) |
\(\cos \theta\) | \(\cos \theta\) \(=\) \(\frac{PR}{RQ}\) | \(\sec \theta\) | \(\sec \theta\) \(=\) \(\frac{RQ}{PR}\) |
\(\tan \theta\) | \(\tan \theta\) \(=\) \(\frac{PQ}{PR}\) | \(\cot \theta\) | \(\cot \theta\) \(=\) \(\frac{PR}{PQ}\) |
Now let us write all the trigonometric ratios with respect to \(\angle Q\) \(=\) \(90^{\circ} - \theta\) in a table.
Table \(2\):
Trigonometric ratio | Relationship with the \(\Delta PQR\) | Trigonometric ratio | Relationship with the \(\Delta PQR\) |
\(\sin (90^{\circ} - \theta)\) | \(\sin (90^{\circ} - \theta)\) \(=\) \(\frac{PR}{RQ}\) | \(\text{cosec}\,(90^{\circ} - \theta)\) | \(\text{cosec}\,(90^{\circ} - \theta)\) \(=\) \(\frac{RQ}{PR}\) |
\(\cos (90^{\circ} - \theta)\) | \(\cos (90^{\circ} - \theta)\) \(=\) \(\frac{PQ}{RQ}\) | \(\sec (90^{\circ} - \theta)\) | \(\sec (90^{\circ} - \theta)\) \(=\) \(\frac{RQ}{PQ}\) |
\(\tan (90^{\circ} - \theta)\) | \(\tan (90^{\circ} - \theta)\) \(=\) \(\frac{PR}{PQ}\) | \(\cot (90^{\circ} - \theta)\) | \(\cot (90^{\circ} - \theta)\) \(=\) \(\frac{PQ}{PR}\) |
Comparing the tables \(1\) and \(2\), we arrive at the following identities.
1. \(\sin \theta\) \(=\) \(\cos (90^{\circ} - \theta)\)
2. \(\cos \theta\) \(=\) \(\sin (90^{\circ} - \theta)\)
3. \(\tan \theta\) \(=\) \(\cot (90^{\circ} - \theta)\)
4. \(\text{cosec}\,\theta\) \(=\) \(\sec (90^{\circ} - \theta)\)
5. \(\sec \theta\) \(=\) \(\text{cosec}(90^{\circ} - \theta)\)
6. \(\cot \theta\) \(=\) \(\tan (90^{\circ} - \theta)\)
Register for free to see more content