PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

4. Trigonometric ratios of 30° and 60°

Consider an equilateral triangle

$ABC$ with sides measuring

$2$ units.

That is

$AB$

$=$

$BC$

$=$

$CA$

$=$

$2$ units.

Draw a bisector of

$\angle A$ such that it meets

$BC$ at

$D$ .

The angle bisector of an equilateral triangle also bisects the side opposite it.

So,

$BD$

$=$

$DC$

$=$

$1$ unit.

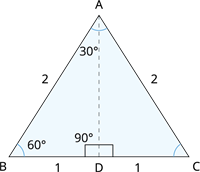
First, let us calculate the measure of angle bisector

$BD$ in the figure.

Consider the triangle

$ABD$ .

Since the given triangle is a right-angled triangle by the Pythagoras theorem, we have:

In a right angled triangle,

$\text{Hypotenuse}^{2} = \text{Adjacent side}^{2} + \text{Opposite side}^{2}$ .

$AB^2$

$=$

$BD^2$

$+$

$DA^2$ .

$DA^2$

$=$

$AB^2$

$-$

$BD^2$

$DA^2$

$=$

$2^2$

$-$

$1^2$

$DA^2$

$=$

$4 - 1$

$DA^2$

$=$

$3$

$\Rightarrow DA$

$=$

$\sqrt{3}$

Therefore, for the considered right-angled triangle, we have:

$30^{\circ}$	$60^{\circ}$
*Opposite side* $=$ $1$ units	*Opposite side* $=$ $\sqrt{3}$ units
*Adjacent side* $=$ $\sqrt{3}$ units	*Adjacent side* $=$ $1$ units
*Hypotenuse* $=$ $2$ units	*Hypotenuse* $=$ $2$ units

Now, let us determine all the trigonometric ratios of

$30^{\circ}$ and

$60^{\circ}$ .

Sine:

$\sin 30^{\circ}$	$\sin 60^{\circ}$
$\sin 30^{\circ}$ $=$ $\frac{\text{Opposite side}}{\text{Hypotenuse}}$ $=$ $\frac{1}{2}$	$\sin 60^{\circ}$ $=$ $\frac{\text{Opposite side}}{\text{Hypotenuse}}$ $=$ $\frac{\sqrt{3}}{2}$

Cosine $30^{\circ}$ :

$\cos 30^{\circ}$	$\cos 60^{\circ}$
$\cos 30^{\circ}$ $=$ $\frac{\text{Adjacent side}}{\text{Hypotenuse}}$ $=$ $\frac{\sqrt{3}}{2}$	$\cos 60^{\circ}$ $=$ $\frac{\text{Adjacent side}}{\text{Hypotenuse}}$ $=$ $\frac{1}{2}$

Tangent:

$\tan 30^{\circ}$	$\tan 60^{\circ}$
$\tan 30^{\circ}$ $=$ $\frac{\text{Opposite side}}{\text{Adjacent side}}$ $=$ $\frac{1}{\sqrt{3}}$	$\tan 60^{\circ}$ $=$ $\frac{\text{Opposite side}}{\text{Adjacent side}}$ $=$ $\frac{\sqrt{3}}{1}$ $=$ $\sqrt{3}$

Using these basic trigonometric ratios determine their reciprocals as follows:

Cosecant:

$\text{cosec}\,30^{\circ}$	$\text{cosec}\,60^{\circ}$
$\text{cosec}\,30^{\circ}$ $=$ $\frac{1}{\sin 30^{\circ}}$ $=$ $\frac{2}{1}$ $=$ $2$	$\text{cosec}\,60^{\circ}$ $=$ $\frac{1}{\sin 60^{\circ}}$ $=$ $\frac{2}{\sqrt{3}}$

Secant:

$\sec 30^{\circ}$	$\sec 60^{\circ}$
$\sec 30^{\circ}$ $=$ $\frac{1}{\cos 30^{\circ}}$ $=$ $\frac{2}{\sqrt{3}}$	$\sec 60^{\circ}$ $=$ $\frac{1}{\cos 60^{\circ}}$ $=$ $\frac{2}{1}$ $=$ $2$

Cotangent:

$\cot 30^{\circ}$	$\cot 60^{\circ}$
$\cot 30^{\circ}$ $=$ $\frac{\text{1}}{\tan 30^{\circ}}$ $=$ $\frac{\sqrt{3}}{1}$ $=$ $\sqrt{3}$	$\cot 60^{\circ}$ $=$ $\frac{\text{1}}{\tan 60^{\circ}}$ $=$ $\frac{1}{\sqrt{3}}$

Let us summarize all the trigonometric ratios of

$30^{\circ}$ and

$60^{\circ}$ in the following table.

	$\sin \theta$	$\cos \theta$	$\tan \theta$	$\text{cosec}\,\theta$	$\sec \theta$	$\cot \theta$
$\theta = 30^{\circ}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$	$2$	$\frac{2}{\sqrt{3}}$	$\sqrt{3}$
$\theta = 60^{\circ}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$	$\frac{2}{\sqrt{3}}$	$2$	$\frac{1}{\sqrt{3}}$

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

4. Trigonometric ratios of 30° and 60°

Theory: