
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoAlgebra is the branch of mathematics that deals with the methods of finding the unknown values by using the variables and constants in the algebraic expression.
Example:
Let's understand this concept with an example:
Kathir went to a shop to buy chocolate. He gave to shop keeper \(₹ 50\) and the shopkeeper gave him \(10\) chocolates.
Now can you find the cost of one chocolate?
If we write this situation in an equation we get,
Let \(x\) be the cost of one chocolate. Then,
.
Therefore the cost of one chocolate is \(₹ 5\).
In this case, we used \(x\) as an unknown value and here this \(x\) is known as variables. We can use the following also as variables to find the unknown values that are
Algebraic expressions:
In the above example, we solved a small equation. But for the complicated equation, one variable and one constant will not be enough to find unknown values. For that, we combine variables and constants using the mathematical operations addition and subtraction to construct algebraic expressions.
Terms, Constants and Variables:
Terms are either variables, numbers or variables multiplied together with numbers. An algebraic operation like addition and subtraction separates terms.
The number of terms: The total number of terms is known as the number of terms of a given expression.
Variable: A variable is a symbol for an unknown value. It is usually denoted in a letter like x, y, a, b.
Constant: A number which stands alone without any variables is known as constant.
Example:
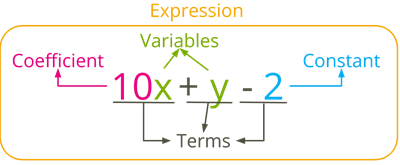
The expression is obtained by adding two parts \(10x\), and \(y\) and by subtracting \(2\).
The variables: Here, the variables are \(x\) and \(y\).
The terms: Here, \(10x\), \(y\) and \(2\) are known as terms.
The number of terms: In this expression, the number of terms is \(3\).
The constant: The term \(2\) is constant.
The coefficient: \(10x\) means \(10\) times \(x\), so \(10\) is a coefficient of \(x\).
Similarly, in the expression of is obtained by adding the two parts \(5a\) and \(9bc\).
The terms: Here, \(5a\) and \(9bc\) are known as terms.
The number of terms: In this expression, the number of terms is \(2\).
The variables: The variables are \(a, b, c\).
The coefficient: The coefficient of \(a\) is \(5\), and the coefficient of \(bc\) is \(9\).