PDF chapter test TRY NOW
A product of numbers, variables and their exponents is called a monomial.
Example:


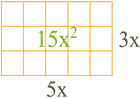
Important!
Typically, we won't keep multiple signs between numerical factors and variables ( \(= 6ay\))
Important!
Note that one variable, such as \(x\), is also considered a monomial, because . A number like \(3\) is also a monomial, because
Some monomials can be simplified.
Example:
Let's simplify the monomial using the exponents' multiplication rule:
\(=\)
(numerical factors are multiplied, but the exponents of the variables are added)
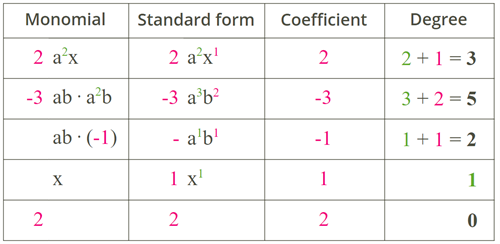
Standard form of a monomial
A monomial is in a standard form, if first there is a constant (numerical) factor, and then variable factors in alphabetical order. If there are several variable factors with the same base, you multiply them, thus you get one factor for each variable.
A monomial is in a standard form, if:
- every product of the same variables is written as one variable with an exponent ;
- a constant factor (or the monomial coefficient) is written as the first term of a monomial.
Example:
The standard form of the monomial is
A constant factor of a standard form of a monomial is called the monomial coefficient.
Example:
The coefficient of the monomial is \(-12\).
Coefficients \(1\) and \(-1\) are not usually written.
Degree of a monomial is the sum of all the exponents of its variable terms (or factors).
Example:
is a seventh degree monomial, because \(4 + 3 = 7\).
Example: