UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreArea of a square: The area of the square is the product (multiply) of the length of its sides.

Area \(=\) side \(×\) side.
Area \((A) = a × a = a²\) square units or \(A = a²\) or \(a² = A\) or \(a = √A\)
Where \(a\) denotes the side of the square.
Side of the square \(= P/4\) units.
Side of the square \(= P/4\) units.
For, diagonals area of square \(= 1/2(d²)\)
The perimeter of a square: The perimeter of a square is the sum of the length of its sides.
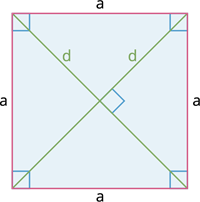
The perimeter \((p) = AB + BC + CD + DA\) or \(p = (a + a + a + a) = 4a\) units.
Where \(a\) denotes the length of each side of a square.
(Note: The perimeter is equal to the sum of all sides).
Diagonals of a square: Diagonals of a square are equal in length, they bisect the angles, and they are the perpendicular bisectors of each other.
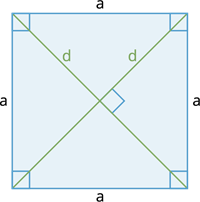
Length of the diagonal \(d = √(a² + a²) = √(2a²^2) = a√2\) units.
Where \(d\) denotes a diagonal of a square is equal to side length times square root of \(2\).