PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA copper wire is connected between the points \(X\) and \(Y\) in the given circuit. Imagine a nichrome wire used instead of copper wire to conduct the experiment, maintaining the same potential difference across the circuit.
Do you think any change will occur in the circuit? If so, what might have changed?
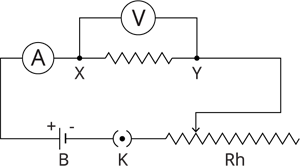
An electric circuit
Yes, there will be a change in the value of the current flowing through the circuit.
Now, change the nichrome wire to an aluminium wire and observe the same. Again, you will notice a different set of current values in the circuit.
The change in the value of current for the same amount of potential difference shows that the resistance varies depending on the material.
A material's resistance is its ability to resist the flow of charges and thus the current flow through it. The value of resistance is different for different materials.
From Ohm's law , the formula of resistance (\(R\)) of any material or a conductor is written as,
The resistance of a conductor can be defined as the ratio between the potential difference across the ends of the conductor and the current flowing through it.
Unit:
The SI unit of resistance is ohm, and it is denoted by .
Resistance of a conductor is said to be one ohm if a current of one ampere flows through it when a potential difference of one volt is maintained across its ends.
Some other units of resistance are:
There are some factors that affect the resistance of a conductor. Let us study these factors in detail in the upcoming section.
Register for free to see more content