PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoYou have studied how plane mirrors create images. You also understand the nature, location, and relative size of the images they produce.
What about the reflections created by spherical mirrors?
For different positions of the object, how can we locate the image formed by a concave mirror?
Is it possible that the images are real or virtual?
Are they bigger, smaller, or the same size as before?
Concave mirror
We will look at this with an activity.
- On a stand, place the concave mirror.
- Make a note of the focal length value (You can also figure it out by capturing the image of a distant object on a piece of paper.)
- Make a chalk line on the table.
- Place the stand so that its pole is directly over the line.
- Draw two more lines parallel to the previous line with chalk so that the distance between any two successive lines equals the mirror's focal length.
- The locations of the points \(P\), \(F\), and \(C\) will now be represented by these lines.
- Remember that the principal focus \(F\) of a spherical mirror with a small aperture is located halfway between the pole \(P\) and the centre of curvature \(C\).
- Maintain a bright object, such as a burning candle, far beyond \(C\). Place a paper screen in front of the mirror and move it around until you get a clear, bright image of the candle flame.
- Take a close look at the image. Make a note of its nature, location, and relative size in relation to the object size.
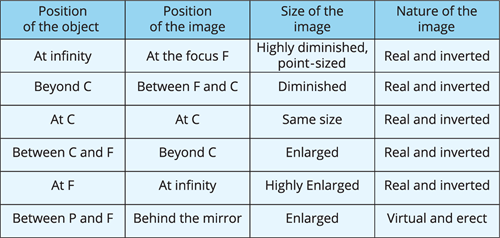
- Place the candle (a) Beyond \(C\), (b) At point \(C\), (c) Between \(F\) and \(C\), (d) At the point \(F\), and (e) between \(P\) and \(F\) to complete the activity.
- Note down and tabulate your observations.
You might not see the image on the screen in one of the cases. Mark the object's location in this case. Then, assume it is a virtual image in the mirror itself.
The nature, position, and size of the image formed by a concave mirror are all dependent on the object's position in relation to points \(P\), \(F\), and \(C\), as demonstrated in the preceding activity. The image is magnified, diminished, or remains the same size depending on the object's position.
The table below provides a summary of these findings.
Register for free to see more content