11. Refractive index

We know that a ray of light travelling obliquely from one transparent medium to another results in the change in its direction in the second medium.

 

The term refractive index can be used to express the magnitude of the change in direction that occurs in a given pair of media.

 

The relative speed of light propagation in different media can be linked to the refractive index, a significant physical quantity. Light propagates at different speeds in different media, as it turns out.
 
In a vacuum, light travels at the fastest speed. When compared to vacuum, the speed of light in air is only slightly slower. In glass or water, it shrinks dramatically.

 

As shown in the figure below, the refractive index value for a given pair of media is determined by the speed of light in the two media.

 

Consider a light ray passing through medium \(1\) and medium \(2\).

 

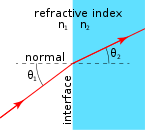
Refraction

 

Consider \(v_1\) the light speed in medium \(1\) and \(v_2\) be the light speed in medium \(2\).

 

The ratio of the speed of light in medium \(1\) to the speed of light in medium \(2\) provides the refractive index of medium 2 with respect to medium 1. The symbol \(n_{21}\) is commonly used to represent it.

This can be expressed mathematically as,

 

\(n_{21}=\frac{Speed\ of\ light\ in\ medium\ 1}{Speed\ of\ light\ in\ medium\ 2}=\frac{v_{1}}{v_{2}}\)

 

By the same argument, the refractive index of medium \(1\) with respect to medium \(2\) is represented as \(n_{12}\). It is given by,

 

\(n_{12}=\frac{Speed\ of\ light\ in\ medium\ 2}{Speed\ of\ light\ in\ medium\ 1}=\frac{v_{2}}{v_{1}}\)

When medium \(1\) is a vacuum or air, the refractive index of medium \(2\) is taken into account in relation to vacuum. This is referred to as the medium's absolute refractive index. \(n_2\) is the simplest way to express it. If \(c\) is the speed of light in air and \(v\) is the speed of light in the medium, then the medium's refractive index is \(n_m\).
 
A medium's absolute refractive index is simply referred to as its refractive index.

 

The refractive index of water is \({n_w}\ =\ 1.33\).

 

This shows that the ratio of light speed in air to light speed in water is equal to \(1.33\). Similarly, crown glass has a refractive index of \({n_w}\ =\ 1.52\).