
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIn the previous sections, we have discussed the structure and working of the human eye. In this section, we will see the defects of the human eye.
All objects between \(25\ cm\) and infinity can be seen clearly by a normal human eye. However, some people's eyes lose their ability to accommodate. This defect can happen for a variety of reasons, including growing older. As a result, their vision is impaired. Let us look at some of the most common human eye defects.
- Myopia
- Hypermetropia
- Presbyopia
- Astigmatism
Myopia:
The lengthening of the eyeball causes myopia, also known as short-sightedness. Nearby objects can be seen clearly with this defect, but distant objects cannot. The distance between the retina and the eye lens is increased, or the focal length of the eye lens is reduced.
As a result, the far point will no longer be infinity for such eyes, and the far point will have moved closer. Due to this, the image of distant objects is formed before the retina. A concave lens can be used to correct this flaw.
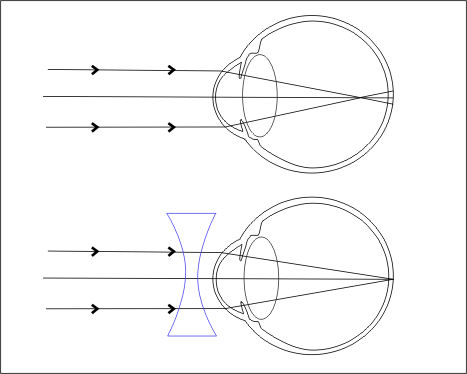
Myopia
Allow a person with myopia to see at a distance of \(x\). Assume he wants to see all objects farther away than this distance, i.e., all the way to infinity. The required concave lens' focal length is then,
\(f\ =\ -x\)
The focal length of the required concave lens if the person can see up to a distance \(x\) and wishes to see up to a distance \(y\) is,
\(f\ =\ \frac{xy}{x-y}\)
Hypermetropia:
The shortening of the eyeball causes hypermetropia, also known as long-sightedness. Distant objects can be seen clearly, but nearby objects cannot be seen clearly due to this defect. The distance between the eye lens and the retina is reduced, or the focal length of the eye lens is increased. As a result, the near point for such eyes will no longer be at \(25\ cm\), and the near point will have moved further. Due to this, the image of nearby objects is formed behind the retina. A convex lens can be used to correct this flaw.

Hypermetropia
Allow a person with hypermetropia to see objects at a distance of \(d\). Assume he wants to see all objects closer than this distance up to \(D\). The focal length of the required convex lens is then calculated,
\(f\ =\ \frac{dD}{d-D}\)