
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoHow is 'work' defined in science?
To understand this, we shall first consider the case when the force is acting in the direction of displacement.
Let us consider,
\(F\) Constant force acting on an object
\(s\) Displacement of the object in the direction of the force.
\(W\) Work done.
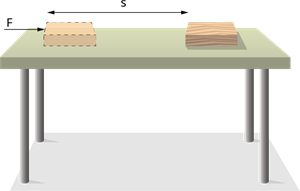
Work is calculated as the product of the force and displacement.
Thus,
Work done by a force acting on an object is equal to the magnitude of the force multiplied by the distance moved in the direction of the force. Work has only magnitude and no direction.
If \(F\) \(=\) \(1\) \(N\), and \(s\) \(=\) \(1\) \(m\) then, the work done by the force will be \(1\) \(Nm\).
Here the unit of work is \(Newton\ metre\) (\(Nm\)) or \(Joule\) (\(J\)).
Thus, \(1\) \(J\) is the amount of Work done on an object when a force of \(1\) \(N\) displaces it by \(1\) \(m\) along the line of action of the force.