PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoApparatus required:
- A source of sound pulses
- A measuring tape
- A sound receiver and
- A stopwatch
Procedure:
- Using the measuring tape, determine the distance '\(d\)' between the source of sound pulse and the reflecting surface.
- The receiver is positioned near the source. The source produces a sound pulse.
- A stopwatch is used to record the time interval between the time the sound pulse is sent and the time the receiver receives the echo. The time interval is denoted by the letter '\(t\)'.
- Carry out the experiment three to four times more. For a given number of pulses, the average time is calculated.
Calculation of sound speed:
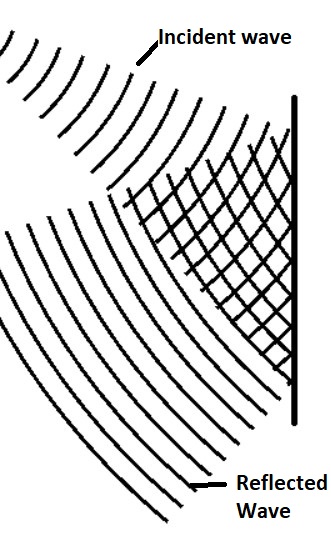
The sound pulse emitted by the source travels a total distance of \(2d\) between the source and the wall before returning to the receiver. The time it takes has been calculated to be \(t\). As a result, the speed of a sound wave is determined by
Reflection of sound waves
Register for free to see more content