Series and parallel connections — lesson. Science State Board, Class 10.

PUMPA - SMART LEARNING

எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்

Book Free Demo

Series connection of parallel resistors:

A series-parallel circuit is formed by connecting a set of parallel resistors in series.

Connect $R_1$ and $R_2$ in parallel to obtain an effective resistance of $R_{P1}$ .
Similarly, connect $R_3$ and $R_4$ in parallel to get an effective resistance of $R_{P2}$ .
These parallel segments of resistors are then joined in series.

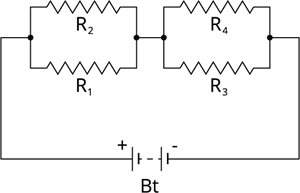
Series-parallel combination of resistors

The formula for the effective resistance of the parallel combination of resistors is

$\frac{1}{R_{P}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}$

For two resistors in the circuit, the effective resistance is given as

$\begin{array}{l} \frac{1}{R_{P1}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} \\ \frac{1}{R_{P2}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} \end{array}$

Using the effective resistance of the series circuit,

$R_{S} = R_{1} + R_{2} + R_{3}$ , the net effective resistance of the series-parallel combination of resistors is,

$R_{Total} = R_{P1} + R_{P2}$

Parallel connection of series resistors:

A parallel-series circuit is formed by connecting a set of series resistors in parallel.

Connect $R_1$ and $R_2$ in series to get an effective resistance of $R_{S1}$ .
Similarly, connect $R_3$ and $R_4$ in series to get an effective resistance of $R_{S2}$ .
These series segments of resistors are then joined in parallel.

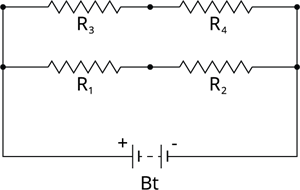
Parallel-series combination of resistors

Using the effective resistance of the series circuit,

$R_{S} = R_{1} + R_{2} + R_{3}$ , we get

$\begin{array}{l} R_{S1} = R_{1} + R_{2} \\ R_{S2} = R_{3} + R_{4} \end{array}$

Using the formula for the effective resistance of the parallel combination of resistors

$\frac{1}{R_{P}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}$ , the net effective resistance of parallel-series combination of resistors is

$\frac{1}{R_{Total}} = \frac{1}{R_{S 1}} + \frac{1}{R_{S 2}}$ .

Did you find an error?

15. Series and parallel connections