
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoGeorg Simon Ohm, a German physicist, conducted various experiments and formulated Ohm's law. The law describes the relationship between potential difference and current.
Ohm's law states that,
At a constant temperature, the steady current '\(I\)' flowing through a conductor is directly proportional to the potential difference '\(V\)' between the two ends of the conductor.
Mathematically, it is written as
Hence,
(or)
The value of the proportionality constant found in the above equation is .
Therefore,
Where \(V\) is the potential difference, \(I\) is the current flowing through a conductor, and \(R\) is the resistance of a material. The resistance is constant for a material (e.g., copper) at a given temperature.
The above equation can also be written as,
In terms of units, the resistance \(R\) of a conductor is said to be \(1\ ohm\) with a potential difference of \(1\ volt\), causing the current of \(1\ ampere\) to flow through the conductor. Then,
Graphical representation:
The graph between the potential difference (\(V\)) and the current (\(I\)) is a straight line for a conductor since \(V\) is proportional to \(I\).
The graph between the potential difference (\(V\)) and the current (\(I\)) is a straight line for a conductor since \(V\) is proportional to \(I\).
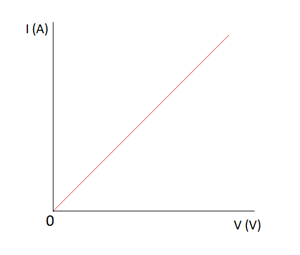
The relation between potential difference and current