
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoIn the previous sections, we learned about linear momentum.
In this section, we will discuss the conservation of linear momentum law and prove them with an example.
Principle of conservation of linear momentum:
There is no change in the linear momentum of a system of bodies as long as no net external force acts on them.
Let us prove the conservation of linear momentum law with the following example.
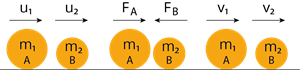
Proof:
Consider two bodies, A and B, having masses and , move with an initial velocity and in a straight line.
Let the initial velocity of the body, A be higher than that of the body, B. i.e., .
During a period of time \(t second\), they tend to have a collision. After the impact, both bodies move along the same straight line with a velocity and , respectively.
Force on body B due to A,
Force on body A due to B,
By Newton’s III law of motion,
\(Action\ force\ =\ Reaction\ force\)
The above equation (eq. 1) confirms in the absence of an external force, the algebraic sum of the momentum after collision is numerically equal to the algebraic sum of the momentum before collision.
Hence, the conservation of linear momentum law is proved.