PDF chapter test TRY NOW
In the previous section, we learned Newton's First Law of motion and the basics of force.
In this section, we will discuss Resultant forces.
Resultant force:
When many forces act simultaneously on the same object, the combined effect of the multiple forces can be represented by a single force, termed as ‘Resultant force’.
The resultant force is equal to the vector sum (adding the magnitude of the forces with their direction) of all the forces.
Consider the number of forces acting on an object and, the resultant force is equal to zero the object will be in the state of equilibrium. Such forces are known as Balanced forces.
If the resultant force is not equal to zero, it changes the motion of a static object or changes the direction of a moving body. The forces that cause the motion of the object is known as Unbalanced forces.
Example:
Force applied with a crowbar, Drawing water from a well, Forces on a weight balance, etc.,
A system or object can be brought to equilibrium by applying another force equal to the magnitude of the resultant force but acts opposite in direction. Such force is known as ‘Equilibrant’.
The below table shows the action of forces and their resultant force.
|
Action of forces
|
Diagram
|
Resultant force
|
|
Parallel forces are acting in the same
direction |
 |
|
|
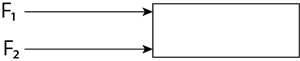Parallel unequal forces are acting in
opposite directions |
 |
|
|
Parallel equal forces are acting in opposite
directions in the same line of action (\(F1 = F2\)) |
 |
Register for free to see more content