PDF chapter test TRY NOW
In the previous section, we learned the basics of mass and weight. In this section, we will discuss apparent weight.
The weight you feel to possess during up and down motion is not the same as your actual weight.
The weight that the body acquires due to the action of gravity and other external forces acting on the body is called Apparent weight.
Let us see this from the following example:
Let us consider a person with mass '\(m\)' is travelling in a lift.
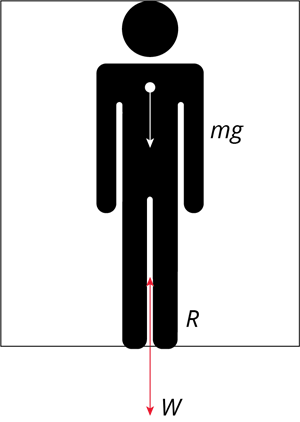
A person in a moving lift
The actual weight of the person is \(W\ =\ mg\), which acts vertically downwards.
The reaction force exerted by the surface of the lift '\(R\)', considered as apparent weight, acts vertically upwards.
Let us see different probabilities of the apparent weight '\(R\)' of the person that arises, based on the movements of the lift, upwards or downwards, which are given in the below table.
|
Position of the lift
|
Case 1: Lift is moving upward with an acceleration '\(a\)'
|
|
Reaction force (\(R\))
|
|
|
Comparison of '\(R\)' with '\(W\)'
|
\(R\ >\ W\)
|
|
Remarks
|
Apparent weight is greater than the actual weight |
|
Position of the lift
|
Case 2: Lift is moving downward with an acceleration '\(a\)'
|
|
Reaction force (\(R\))
|
|
|
Comparison of '\(R\)' with '\(W\)'
|
\(R\ <\ W\)
|
|
Remarks
|
Apparent weight is lesser than the actual weight |
|
Position of the lift
|
Case 3: Lift is at rest
|
|
Reaction force (\(R\))
|
|
|
Comparison of '\(R\)' with '\(W\)'
|
\(R\ =\ W\)
|
|
Remarks
|
Apparent weight is equal to the actual weight. |
|
Position of the lift
|
Case 4: Lift is falling down freely
|
|
Reaction force (\(R\))
|
|
|
Comparison of '\(R\)' with '\(W\)'
|
\(R\ =\ 0\)
|
|
Remarks
|
Apparent weight is equal to zero. |
