Principle of conservation of linear momentum — lesson. Science State Board, Class 10.

PDF chapter test TRY NOW

In the previous sections, we learned about linear momentum.

In this section, we will discuss the conservation of linear momentum law and prove them with an example.

Principle of conservation of linear momentum:

There is no change in the linear momentum of a system of bodies as long as no net external force acts on them.

Let us prove the conservation of linear momentum law with the following example.

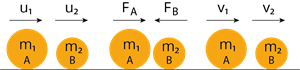
Proof:

Consider two bodies, A and B, having masses

m_{1}

and

m_{2}

, move with an initial velocity

u_{1}

and

u_{2}

in a straight line.

Let the initial velocity of the body, A be higher than that of the body, B. i.e.,

u_{1} ≻ u_{2}

During a period of time \(t second\), they tend to have a collision. After the impact, both bodies move along the same straight line with a velocity

v_{1}

and

v_{2}

, respectively.

Force on body B due to A,

F_{B} = \frac{m_{2} (v_{2} - u_{2})}{t}

Force on body A due to B,

F_{A} = \frac{m_{1} (v_{1} - u_{1})}{t}

By Newton’s III law of motion,

\(Action\ force\ =\ Reaction\ force\)

\begin{array}{l} F_{A} = - F_{B} \\ \frac{m_{1} (v_{1} - u_{1})}{t} = - (\frac{m_{2} (v_{2} - u_{2})}{t}) \\ \frac{{(m}_{1} v_{1}) - (m_{1} u_{1})}{t} = - (\frac{{(m}_{2} v_{2}) - (m_{2} u_{2})}{t}) \\ Remove " t " from bothsides, \\ {(m}_{1} v_{1}) - (m_{1} u_{1}) = - ({(m}_{2} v_{2}) - (m_{2} u_{2})) \\ {(m}_{1} v_{1}) - (m_{1} u_{1}) = - {(m}_{2} v_{2}) + (m_{2} u_{2}) \\ {(m}_{1} v_{1}) + {(m}_{2} v_{2}) = (m_{1} u_{1}) + (m_{2} u_{2}) - (eq . 1) \end{array}

The above equation (eq. 1) confirms in the absence of an external force, the algebraic sum of the momentum after collision is numerically equal to the algebraic sum of the momentum before collision.

Hence, the conservation of linear momentum law is proved.

Previous theory

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

17. Principle of conservation of linear momentum

Theory: