
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoAtomic mass unit:
Atomic mass unit (u) is defined as \(1/12\)\(^{th}\) of the mass of a neutral carbon atom \(_{6}C^{12}\) (carbon – 12 atom). This unit is used to measure the mass of an atom.
Thus, the mass of a carbon atom is \(12\ u\).
Estimation of mass of helium nucleus:
Consider a helium atom \(_{2}He^{4}\), which has \(2\) electrons, \(2\) protons and \(2\) neutrons.
Consider a helium atom \(_{2}He^{4}\), which has \(2\) electrons, \(2\) protons and \(2\) neutrons.
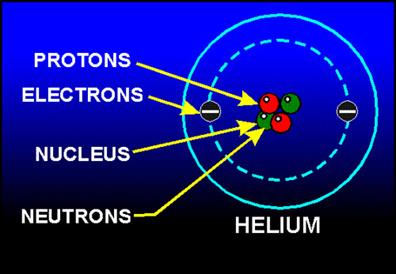
Helium atom
Mass of a proton \(=\ 1.0078\ u\)
Mass of a neutron \(=\ 1.0087\ u\)
But experimentally, the actual mass of a helium nucleus is \(4.0026\ u\). So, what happened to the remaining mass of \(0.0304\ u\)?
To know that, we need to look at the concept of the mass defect.
Mass defect:
The mass of the daughter nucleus formed during a nuclear reaction (fission and fusion) is lesser than the sum of the masses of the two-parent nuclei. This difference in mass is called the mass defect.
In the above example, the mass defect is found to be \(0.0304\ u\).
Unit of energy:
In nuclear physics, the electron volt (\(eV\)) is the unit used to measure the energy of tiny particles. It is the energy of an electron when it is accelerated by an electric potential of one volt.
\(1\ eV\) \(=\) \(1.602 \times{10^{-19}}\) \(joule\)
\(1\ million\ electron\ volt\) \(=\) \(1\ MeV\) \(=\) \(10^6\ eV\) (\(mega\ electron\ volt\))
Generally, the energy of about \(200\ MeV\) is released in a nuclear fission process.
Einstein's mass-energy equivalence:
According to the mass-energy equivalence, the mass is converted into energy and vice versa. Albert Einstein proposed the concept of mass-energy equivalence in \(1905\).
The relation between mass and energy is
\(E = mc^2\)
Where \(E\) is the energy, \(m\) is the mass, and \(c\) is the velocity of light in a vacuum, which is equal to \(3 \times {10^8}\ ms^{-1}\).
According to Einstein, mass and energy are not independent but are mutually convertible. A body that changes its energy '\(E\)' undergoes a change in its mass, '\(m\)'. For example, if the energy of a particle is increased, its mass also increases.
Binding energy:
Binding energy holds the nucleons (protons and neutrons) of a nucleus together, even from the loss in the total mass of the nucleons (mass defect). It is measured in \(MeV\).
Where \(Δm\) is the mass defect of the nucleus in atomic mass units ‘\(u\)’.
The higher the binding energy per nucleon, the greater is the stability of the atom. Also,
Where \(A\) is the mass number of an element.
Reference:
https://live.staticflickr.com/5005/5351051490_483f3695b0.jpg