
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoThe volume of irregularly shaped objects
There is no exact formula to measure irregularly shaped objects, but there are some methods to do it. Since volume is the total space occupied by an object, the volume of a small irregular piece of stone can be found by the water displacement method.
Water displacement method
The volume is determined using a measuring cylinder, a piece of stone and water.
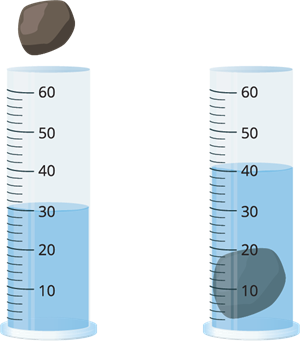
Measuring cyliner
- A measuring cylinder with markings is filled with \(150\ ml\) of water.
- A stone is tied with a piece of thread and immersed completely into the water.
- When the stone is immersed, the level of water eventually increases.
- The stone occupies the space inside the cylinder by displacing some amount of water. This makes the water level rise.
Inference
The volume of water displaced will be equal to the volume of space occupied by the stone in the container. This technique is known as the water displacement method and was found by Archimedes.
Amount of water displaced by the stone
Assume that the water level was \(150\ ml\) initially. After immersing a piece of stone, imagine the water level rises to \(180\ ml\). Then,
Volume of the water displaced \(=\) \(180\ ml\) \(-\) \(150\ ml\) \(=\) \(30\ ml\)
\(1\ ml\) \(=\) \(1\ cm^3\)
\(30\ ml\) \(=\) \(30\ cm^3\)
Volume of stone \(=\) \(30\ cm^3\)
\(30\ ml\) \(=\) \(30\ cm^3\)
Volume of stone \(=\) \(30\ cm^3\)
Volume of gas
Like liquids, gases also fill the container into which they are placed. However, gases can be compressed and can be made to occupy lesser space - for example, an LPG gas cylinder. Hence, calculating the volume of gas is different from that of the volume of solids and liquids.
Liquids and gases can be measured in \(litres\) and can be expressed in \(cubic\) \(metre\) or \(m^3\).
Important!
One of the tiny unit for the measurement of liquid is \(microlitre\) ().
Think and answer!
It is not easy to guess which vessel has more water by simply looking at it. In general, graduated cylinders, graduated containers, beakers, pipettes and burettes are used to measure the volume of the liquid.

Different types of containers with water molecules to measure
In this case, We shall use the beakers to measure the volume of the water.

Measuring jar
Initially, the liquid in the first container is poured into a beaker, and the reading is taken. The exact process can be repeated for the other containers too. By comparing the results, We shall find the container which has more volume of water.
Reference:
https://upload.wikimedia.org/wikipedia/commons/1/17/Displacement_measurement.png