PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoAeroplanes, aircrafts and ships maintain not only their speed but also their direction.
For example, take a ship; it has to maintain its speed and direction, and that's where average velocity concepts come into play. Similar to the average speed, we can also define average velocity.
Average velocity
Average velocity can be defined as the ratio between the total displacement and the total time taken.
Zero displacement
In some circumstances, the displacement can be zero. Let us take an example to understand this clearly.
Consider that you are a formula one race car driver; you finished a \(250\) \(km\) race in \(one\ hour\ and\ thirty\ minutes\). You finished the race at same place where you started.
Then, what will be your average velocity?
We know that,
\(Average\ velocity\)
In this case, first we need to find the displacement. But, the important thing is your starting and finishing points are the same. Therefore, the displacement will be zero.
If the displacement is zero, then the average velocity is also zero.
Important!
Note: If the initial and final point of an object is in the same point, then the displacement is zero, as there is no displacement that occurred.
Relation between \(v\), \(d\) and \(t\):
The below triangle diagram can help you to recall the relationship between velocity (\(v\)), displacement (\(d\)), and time(\(t\)).
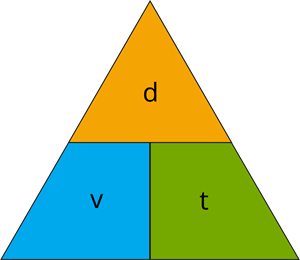
The relation is,
Therefore, simply we can write .
Register for free to see more content