PDF chapter test TRY NOW
All the materials do not have the same density. Depending on the nature of the material, the density varies.
Materials with a higher density are referred to as denser, while those with a lower density are rarer. For example, water is a denser material with high density, and the air is rarer with low density.
Relationship between the density, mass and volume
We can find the mass and volume of an object with the help of the density formula.
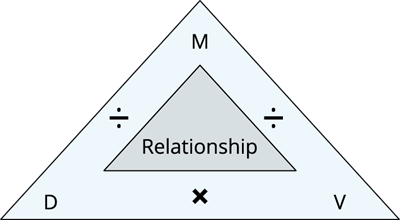
The pictorial representation of the formula is shown below as a density triangle.
Density of substances at room temperature
The table below shows the nature of different materials with their respective densities.
Nature | Material | Density in \(kg/ m^3\) |
Gas | Air | \(1.2\) |
Liquid | Kerosene | \(800\) |
Liquid | Water | \(1,000\) |
Liquid | Mercury | \(13,600\) |
Solid | Wood | \(770\) |
Solid | Aluminium | \(2700\) |
Solid | Iron | \(7,800\) |
Solid | Copper | \(8,900\) |
Solid | Silver | \(10,500\) |
Solid | Gold | \(19,300\) |
We can find the mass and volume of the materials from these density values.
Solved examples
1. Find the volume of an iron sphere having a mass of \(2000\) \(kg\). [Density of iron is \(7800\) \(kg/m^3\)].
Mass of iron sphere \(=\) \(2000\) \(kg\)
Density of iron \(=\) \(7800\) \(kg/m^3\)
Thus, the volume of an iron sphere is \(0.25\ m^3\).
2. A wooden box has a volume of \(200\ cm^3\). Calculate the mass of the wooden box with a density of \(0.77\) \(g/cm^3\).
Volume of the box \(=\) \(200\ cm^3\)
Density of wood \(=\) \(0.77\) \(g/cm^3\)
Therefore, the mass of the wooden box is \(154\ g\).
Important!
Units of the density value should be converted according to the problems.
3. A solid aluminium can of mass \(100\ g\) has a volume of \(500\ cm^3\). Find the density of the can.
Mass of the aluminium can \(=\) \(100\) \(g\)
\(\)
\(\)
Volume of the aluminium can \(=\) \(500\ cm^3\)
Hence, the density of the aluminium can is found to be \(0.2\ g/cm^3\).
Register for free to see more content