PDF chapter test TRY NOW
Let us now discuss few key concepts which are needed to study image formation by a spherical mirror.
The mirror is assumed to be rotationally symmetric about this axis. Hence, we can represent a three-dimensional mirror in a two-dimensional diagram without losing generality.
Centre of Curvature:
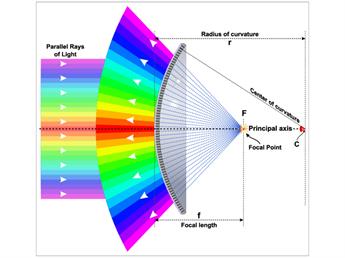
It is the midpoint (centre) of the sphere from which the mirror is made. It is represented by the letter "C" in the ray diagrams.
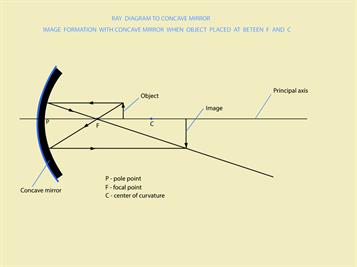
Note: A ray diagram represents the formation of an image by the spherical mirror. You will study about them in higher classes.
Pole:
It is the geometric centre of the spherical mirror. It is denoted by the letter "P".
Radius of Curvature:
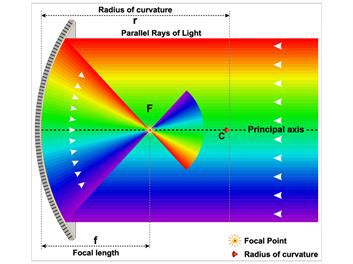
It is the distance between the centre of the sphere and the vertex. It is represented by the letter "R" in ray diagrams.
(The vertex is the point on the mirror’s surface where the principal axis coincides (meets) with the mirror. It is also called as ‘pole’).
Principal Axis:
The line that connects the pole of the mirror and its centre of curvature is called principal axis.
Focus:
When a beam of light falls on a spherical mirror, the reflected rays converge (concave mirror) at or seem to diverge from (convex mirror) a point on the principal axis. This point is known as the 'focus' or 'principal focus'. It is also called as the focal point. It is denoted by the letter "F" in ray diagrams.
Focal length:
The distance between the pole and the principal focus is known as the focal length (f) of a spherical mirror. There is a relation between the focal length of a spherical mirror and its radius of curvature.
The focal length is half of the radius of curvature.