
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA sound wave can be explained completely by five characteristics; they are
- Amplitude
- Frequency
- Time period
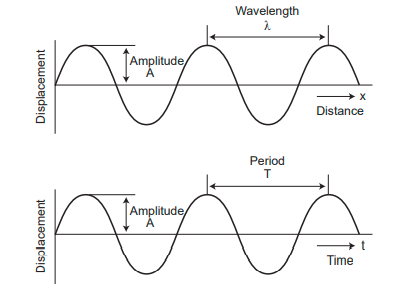
- Wavelength
- Velocity or speed
Wave nature
Amplitude (\(A\)):
The wave's amplitude is the maximum displacement of medium particles from their original undisturbed positions when a wave passes through the medium. The sound will be loud if the vibration of a particle has a large amplitude and soft if the vibration has a small amplitude. 'A' stands for amplitude. The \(metre\) \(m\) is its SI unit.
Time period (\(T\)):
The time taken for one complete oscillation of a sound wave is called the time period of the sound wave.
Frequency (\(F\)):
The number of oscillations an object takes per second is called its frequency.
The SI unit of frequency is \(Hertz\) (\(Hz\)).
The SI unit of frequency is \(Hertz\) (\(Hz\)).
Velocity or Speed of the sound (\(v\)):
The speed of sound is defined as the distance that sound travels in one second. The letter ‘\(v\)' stands for it.
It is mathematically represented as,
where '\(n\)' is the frequency and '' is the wavelength.
Distance travelled by the sound wave is found by,
Example:
A sound has a frequency of \(70\) \(Hz\) and a wavelength of \(10\) \(m\). What is the speed of the sound?
Solution:
Frequency (\(n\)) \(=\) \(70\) \(Hz\)
Wavelength (\(λ\)) \(=\) \(10\) \(m\)
To find: Speed of the sound (\(v\))
We know the formula,
By applying these values we get,
\(v\) \(=\)
\(v\) \(=\) 700