PDF chapter test TRY NOW
முந்தைய பகுதிகளில், நியூட்டனின் பொது ஈர்ப்பியல் விதி பற்றி படித்தோம்.
இந்தப் பகுதியில், புவிஈர்ப்பு முடுக்கம் பற்றி அறிந்துகொள்வோம்.
புவிஈர்ப்பு முடுக்கம்(g):
நீங்கள் எந்த ஒரு பொருளை மேல்நோக்கி எறிந்தாலும் புவிஈர்ப்பு விசையின் தாக்கத்தால், அதன் திசைவேகம் படிப்படியாக குறையும். அம்மதிப்பு ஒரு குறிப்பிட்ட உயரத்தில் முழுமையாக சுழி ஆகிறது.
ஈர்ப்பு விசையினால் கீழே விழும் போது அதன் திசைவேகம் தொடர்ந்து மாற்றம் பெறுகிறது. இது அப்பொருளுக்கு முடுக்கத்தினை ஏற்படுத்தும். இம்முடுக்கம் புவிஈர்ப்பு விசையினால் ஏற்படுவதால் புவிஈர்ப்பு முடுக்கம் என்றழைக்கப்படுகிறது.
புவி ஈர்ப்பு முடுக்கத்தின் சராசரி மதிப்பு (கடல் மட்டத்தில்) \(9.8\ \text{மீ வி}^{-2}\) ஆகும்.
இதன் பொருளானது, தடையின்றி கீழே விழும் பொருளின் திசைவேகம், ஒரு வினாடிக்கு \(9.8\ \text{மீ வி}^{-1}\) என்ற அளவில் மாற்றம் பெறும் என்பதாகும். ‘\(g\)’ இன் மதிப்பு புவியில் அனைத்து இடங்களிலும் ஒரே மதிப்பாய் இருக்காது.
\(g\) மற்றும் \(G\) இவற்றிற்கிடையே உள்ள தொடர்பு:
புவி பரப்பின் மீது \(m\) என்ற நிறையுள்ள பொருள் ஒன்று ஓய்வு நிலையில் உள்ளதாக கொள்வோம். பொருளின் மீது செயல்படும் இரு விசைகளை கீழ் கண்டவாறு கணக்கிடலாம்.
புவியின் நிறையை \(M\) எனக் கொள்வோம்.
புவி மையத்தில் புவியின் நிறை குவிந்திருப்பதாக எடுத்துக் கொள்வோம்.
புவியின் ஆரம் \(R\ =\ 6378\ \text{கி. மீ}\) (தோராயமாக \(=\ 6400\ \text{கி. மீ}\)) ஆகும்.
நியூட்டனின் பொது ஈர்ப்பியல் விதிப்படி,
புவிக்கும் பொருளுக்கும் உள்ள ஈர்ப்பு விசை,
\(F\ =\ \frac{G \times M \times m}{R^2}\) - (1)
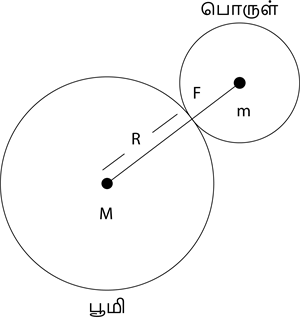
இதே போல் பொருள் மீது செயல்படும் விசை மதிப்பை நியூட்டனின் இரண்டாம் விதிப்படி கணக்கிடலாம்.
இவ்விதிப்படி விசையானது பொருளின் நிறைக்கும், முடுக்கத்திற்கும் உள்ள பெருக்கற்பலனாகும்.
இங்கு பொருளின் முடுக்கம், புவியின் ஈர்ப்பு முடுக்கத்திற்கு சமமாக இருப்பதால் (\(a\ =\ g\))
\(F\ =\ m \times a\ =\ m \times g\ (\text{எடை})\) - (2)
சமன்பாடுகள் (1) மற்றும் (2) னை சமன் செய்ய,
\(m \times g\ =\ \frac{G \times M \times m}{R^2}\)
எனவே புவி ஈர்ப்பு முடுக்கம்,
\(g\ =\ \frac{G \times M}{R^2}\)
இச்சமன்பாடு ‘\(g\)’ மற்றும் ‘\(G\)’ இவற்றிற்கிடையே உள்ள தொடர்பினை அளிக்கிறது.
Register for free to see more content