PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoஇப்பகுதியில் பாரன்ஹீட், செல்சியஸ் மற்றும் கெல்வின் அளவீட்டிற்கும் உள்ள தொடர்பை பற்றி அறிந்துக் கொள்ளப் போகிறோம்.
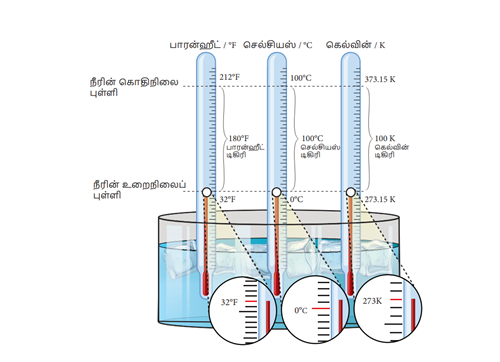
பாரன்ஹீட் - செல்சியஸ் - கெல்வின்
பாரன்ஹீட் அளவீட்டிற்கும் செல்சியஸ் அளவீட்டிற்கும் உள்ள தொடர்பும் கீழே கொடுக்கப்பட்டுள்ளது.
\(\frac{\text{(F-32)}}{\text{9}}\) \(=\) \(\frac{\text{C}}{\text{5}}\)
கெல்வின் அளவீட்டிற்கும் செல்சியஸ் அளவீட்டிற்கும் உள்ள தொடர்பும் கீழே கொடுக்கப்பட்டுள்ளது.
\(K\) \(=\) \(273.15\) \(+\) \(C\)
சில பொருள்களின் வெப்பநிலைகள் செல்சியஸ் அளவீட்டு முறையில் கீழே கொடுக்கப்பட்டுள்ளன அவைகள் முறையே
| வெப்பநிலை | செல்சியஸ் அளவீட்டு முறை \((°C)\) |
| நீரின் கொதிநிலை | \(100\) |
| நீரின் உறைநிலை | \(0\) |
| மனித உடலின் சராசரி வெப்பநிலை | \(37\) |
| அறை வெப்பநிலை (சராசரி) | \(72\) |
சில பொருள்களின் வெப்பநிலைகள் பாரன்ஹீட் அளவீட்டு முறையில் கீழே கொடுக்கப்பட்டுள்ளன அவைகள் முறையே
| வெப்பநிலை | பாரன்ஹீட் அளவீட்டு முறை \((° F)\) |
| நீரின் கொதிநிலை | \(373.15\) |
| நீரின் உறைநிலை | \(273.15\) |
| மனித உடலின் சராசரி வெப்பநிலை | \(310.15\) |
| அறை வெப்பநிலை (சராசரி) | \(296.15\) |
சில பொருள்களின் வெப்பநிலைகள் கெல்வின் அளவீட்டு முறையில் கீழே கொடுக்கப்பட்டுள்ளன அவைகள் முறையே
| வெப்பநிலை | கெல்வின் அளவீட்டு முறை \((K)\) |
| நீரின் கொதிநிலை | \(212\) |
| நீரின் உறைநிலை | \(32\) |
| மனித உடலின் சராசரி வெப்பநிலை | \(98.6\) |
| அறை வெப்பநிலை (சராசரி) | \(23\) |
- உலகின் பெரும்பான்மையான மனிதர்கள் அன்றாட வாழ்வில் வெப்பநிலைகளை அளக்க செல்சியஸ் அளவீட்டு முறையினை பயன்படுத்துகின்றார்கள்.
- கெல்வின் அளவீட்டு முறையானது தனிச்சுழி அளவீட்டு முறை மட்டும் கிடையாது.
- \(1\) \(°\)\(C\) வெப்பநிலை மாற்றம் ஏற்பட்டால் \(1\) \(K\) வெப்பநிலை மாறுபாடு ஏற்படும் வகையில் கெல்வின் அளவீட்டு முறை வடிவமைக்கப்பட்டு உள்ளது.
- இதன் மூலம் \(273.15\) என்ற மதிப்பினை செல்சியஸ் அளவீட்டுடன் கூட்டுவதன் மூலமாகவோ அல்லது கழிப்பதன் மூலமாகவோ நாம் மிக எளிமையாக செல்சியஸ் அளவீட்டு முறையினை தனிச்சுழி அளவீட்டு (கெல்வின்) முறைக்கு மாற்றிக் கொள்ள முடியும்.
- ஐக்கிய அமெரிக்க நாடுகளில் பாரன்ஹீட் அளவீட்டு முறையினை பயன்படுத்துகின்றனர். பாரன்ஹீட் அளவீட்டு முறையினை தனிச்சுழி ( கெல்வின் ) அளவீட்டு முறைக்கு மாற்றுவது எளிமையானதாக இல்லை. இதனை சரி செய்ய அவர்கள் ரான்கீன் அளவீட்டு முறையினை பயன்படுத்துகின்றனர்.
- கிளாஸ்கோ பல்கலைக்கழகத்தின் பொறியியலாளர் மற்றும் இயற்பியலாளரான ரான்கீன் \(1859\) ஆம் ஆண்டு இம்முறையினை அறிமுகப்படுத்தினார். இது தனிச்சூழி அளவீட்டு முறையாகும்.
- \(1\)\(°\)\(R\) ல் ஏற்படும் மாற்றம் \(1\)\(°\)\(F\) க்கு சமமாகும் வகையில் வடிவமைக்கப்பட்டு உள்ளது.
- எனவே பாரன்ஹீட் அளவீட்டு முறையினை பயன்படுத்துபவர்களுக்கு தனிச்சுழி அளவீட்டு முறை தேவைப்பட்டால் அவர்கள் \(R\) \(=\) \(F\) \(+\) \(459.67\) என்ற வாய்ப்பாட்டினை பயன்படுத்தி ரான்கீன் முறைக்கு மதிப்பினை எளிமையாக மாற்றிக்கொள்ள இயலும்.
Register for free to see more content