
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoஒரு தளக்கோணம் என்பது இரண்டு நேர் கோடுகள் அல்லது இரண்டு தளங்கள் சந்திக்கும் கோணம். இது இரண்டு பரிமாணங்களைக் கொண்டுள்ளது. ரேடியன் என்பது தளக்கோணத்தின் \(SI\) அலகு. மேலும், இது rad எனக் குறிக்கப்படுகிறது.
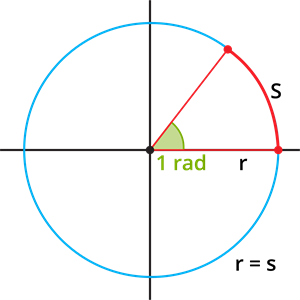
வட்டத்தின் ஆரத்திற்கு சமமான நீளம் கொண்ட ஒரு வளைவின் மையத்தில் உள்ள கோணம் ரேடியன் எனப்படும்.
எனில்,
கோணங்களை அளவிட ரேடியன்கள் பயன்படுத்தப்படுகின்றன. மேலே கொடுக்கப்பட்டுள்ள சமன்பாடுகளை பயன்படுத்தி ரேடியன் அடிப்படையில் ஒரு மதிப்பை டிகிரிகளாகவும் நேர்மாறாகவும் மாற்றலாம்.
கணக்கீடு: \(60°\) என்பதை ரேடியனாக மாற்றுக.
தீர்வு:
ரேடியனுக்கும் டிகிரிக்கும் உள்ள தொடர்பு பின்வருமாறு:
கணக்கீடு: \(π/4 rad\) - ஐ டிகிரியாக மாற்றுக.
தீர்வு
ரேடியனுக்கும் டிகிரிக்கும் உள்ள தொடர்பு பின்வருமாறு:
எனில்:
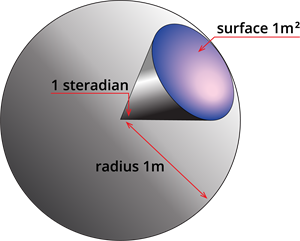
திடமான கோணம் என்பது ஒரு பொதுவான புள்ளியில் சந்திக்கும் மூன்று அல்லது அதற்கு மேற்பட்ட தளங்களில் உருவாகும் கோணம். இது கூம்பின் உச்சியில் உருவாகும் கோணம் என்றும் அழைக்கப்படுகிறது. ஸ்ட்ரேடியன் என்பது திட கோணத்தின் SI அலகு. மேலும் இது 'sr' எனக் குறிக்கப்படுகிறது.
உங்களுக்கு தெரியுமா?
முன்னதாக, தளக்கோணமும் திடக் கோணமும் துணை அளவுகளாகக் கருதப்பட்டன. ஆனால், அவை \(1995\)-இல் பெறப்பட்ட அளவுகளாக மாற்றப்பட்டன.
ஸ்ட்ரேடியன் என்பது ஒரு கோளத்தின் மையத்தில் உள்ள ஒரு திடமான கோணம் ஆகும். அதன் புறப்பரப்பு, கோளத்தின் ஆரத்தின் இருமடிக்குச் சமமாக இருக்கும் ஒரு பகுதியால் இணைக்கப்பட்டுள்ளது. இது மூன்று பரிமாணங்களைக் கொண்டுள்ளது.