PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoவறையரை:
\(A\), \(B\) and \(C\) ஆகியவை வெற்றில்லா கணங்கள் எனில், அதன் கார்டீசியன் பெருக்கற்பலனில் கணமானது அனைத்து சாத்தியமான வரிசையில் அமைந்த மூன்றின் தொகுதிகளின் கணமாகும். அதனை \(A \times B \times C\) \(=\) \(\{(a, b, c) \text{ அனைத்து } a \in A, b \in B, c \in C\}\).
பட விளக்கம்:
இரண்டு மற்றும் மூன்று கணங்களின் கார்ட்டீசியன் பெருக்களின் வடிவியல் புரிதலுக்கு பின்வரும் எடுத்துக்காட்டைப் பார்ப்போம்.
கணங்கள் \(A\), \(B\) மற்றும் \(C\) என்க.
இங்கு \(A\) \(=\) \(\{2, 3\}\), \(B\) \(=\) \(\{2, 3\}\) மற்றும் \(C\) \(=\) \(\{2, 3\}\).
முதலில், \(A \times B\) இன் பெருக்கற்பலணைக் காணலாம்.
\(A \times B\) \(=\) \(\{2, 3\} \times \{2, 3\}\)
\(A \times B\) \(=\) \(\{(2 ,2), (2, 3), (3, 2), (3, 3)\}\)
பெருக்கற்பலன் \(A \times B\) இன் வடிவியல் பட விளக்கம்:
 |
இங்கு, இரு கணங்களின் பெருக்கற்ப்பலனை \(xy\) \(-\) தளத்தில் குறிக்கப்பட்டுள்ளது.
\(A \times B\) இன் பெருக்கற்பலன் இரு பரிமாணங்களைக் கொண்ட சதுர வடிவத்தை ஏற்படுதிதியுள்ளது.
இப்பொழுது, \(A \times B \times C\) இன் பெருக்கற்பலணைக் காணலாம்.
\(A \times B \times C\) \(=\) \((A \times B) \times C\)
\(A \times B \times C\) \(=\) \(\{(2 ,2), (2, 3), (3, 2), (3, 3)\}\) \(\times\) \(\{2, 3\}\)
\(A \times B \times C\) \(=\) \(\{(2 ,2, 2), (2 ,2, 3), (2, 3, 2), (2, 3, 3), (3, 2, 2), (3, 2, 3), (3, 3, 2), (3, 3, 3)\}\).
பெருக்கற்பலன் \(A \times B \times C\) இன் வடிவியல் பட விளக்கம்:
 |
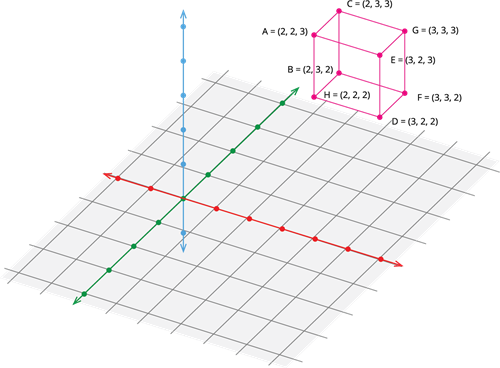இங்கு, மூன்று கணங்களின் பெருக்கற்ப்பலனை \(xyz\) \(-\) வெளியில் குறிக்கப்பட்டுள்ளது.
\(A \times B \times C\) இன் பெருக்கற்பலன் முப்பரிமாணங்களைக் கொண்ட கனச்சதுர வடிவத்தை ஏற்படுதிதியுள்ளது.
Important!
இரண்டு வெற்றில்லா கணங்களின் கார்டீசியன் பெருக்கல் இரு பரிமாணங்களைக் கொண்ட வடிவத்தை ஏற்படுத்தும், அதேபோல் மூன்று வெற்றில்லா கணங்களின் கார்டீசியன்
பெருக்கல் மூன்று பரிமாணங்களைக் கொண்ட முப்பரிமாணப் பொருளை ஏற்படுத்தும்.
பெருக்கல் மூன்று பரிமாணங்களைக் கொண்ட முப்பரிமாணப் பொருளை ஏற்படுத்தும்.
Register for free to see more content