PDF chapter test TRY NOW
a மற்றும் b -க்கு இடையே உள்ள வித்தியாசம் n -யின் மடங்கு
எனில் மட்டு n -யின் அடிப்படையில் a யும் b யும் ஒருங்கிசைவு உடையதாகும். அதாவது a-b= kn, k \mathbb{Z} இதை a \equiv b (\textit{மட்டு} \ n) எனவும் எழுதலாம். இங்கு n என்பது மட்டு எண் என அழைக்கப்படுகிறது.
Example:
39 \equiv 4 (\textit{மட்டு} \ 5). இங்கு, என்பது மட்டு ஏனெனில் 39 - 4 = 35 ஆனது 5 ஆல் வகுப்படும்.
கீழ்கண்ட எடுத்துக்காட்டுகளைக் காண்போம்.
Example:
1. 3 (\textit{மட்டு} \ 2) மதிப்பு காண்க.
தீர்வு:
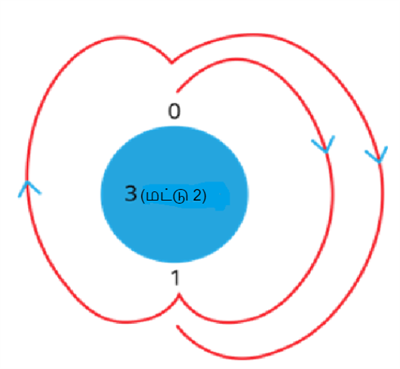
மட்டு 2 எனும்போது 0 மற்றும் 1 ஆகியன மீதியாகக் கிடைக்கலாம்.
கொடுக்கப்பட்ட எண்ணின் மீதியைக் கண்டறிய, 0 இலிருந்து தொடங்கி 3 எண்கள் வழியாக கடிகார திசையில் செல்லவும். 3 எண்கள் 0 தொடங்கி ஒரு சுழற்சியில் செல்லும். அவை 1, 0, 1. 1 இன் மீதியில் சுழற்சி முடிவதால், 3 (\textit{மட்டு} \ 2)க்கான பதில் 1 ஆகும்.
எனவே, 3 \equiv 1 (\textit{மட்டு} \ 2)
2. -3 (\textit{மட்டு} \ 2) இன் மதிப்பு காண்க.
தீர்வு:
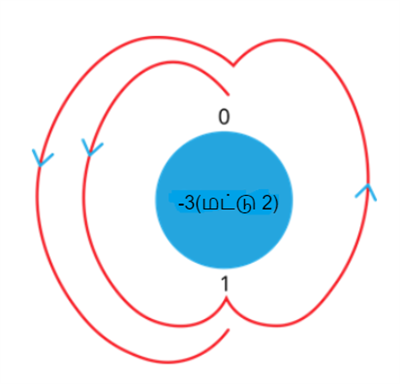
மட்டு 2 இன் மீதிகள் 0 மற்றும் 1 என இருக்கலாம்.
கொடுக்கப்பட்ட எண்ணின் மீதியைக் கண்டறிய, 0 இலிருந்து தொடங்கி, 3 எண்களை எதிர் கடிகார திசையில் செல்லவும் (எண்ணில் எதிர்மறை அடையாளம் இருப்பதால்). 3 எண்கள் 0 தொடங்கி ஒரு சுழற்சியில் செல்லும். அவை 1, 0, 1. 1 இன் மீதியில் சுழற்சி முடிவதால், -3 (\textit{மட்டு} \ 2)க்கான பதில் 1 ஆகும்.
எனவே, -3 \equiv 1 (\textit{மட்டு} \ 2)
Register for free to see more content