PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demo\(x\), \(y\) மற்றும் \(z\) என்ற மூன்று மாறிகளில் அமைந்த ஒருபடிச் சமன்பாடு, மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாடு எனப்படும்.
மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டின் பொது வடிவமானது,
\(ax + by + cz + d = 0\)
இங்கு, \(a\), \(b\), \(c\) மற்றும் \(d\) ஆகியவை பூஜ்ஜியமற்ற மெய் எண்கள், மற்றும் \(x\) மற்றும் \(y\) ஆகியவை மாறிகள் .
வரைபட முறை:
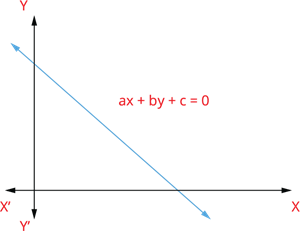
இரு மாறிகளில் அமைந்த நேரிய சமன்பாடு \(ax + by + c = 0\) ஆனது நேர்க்கோட்டை குறிக்கும்.
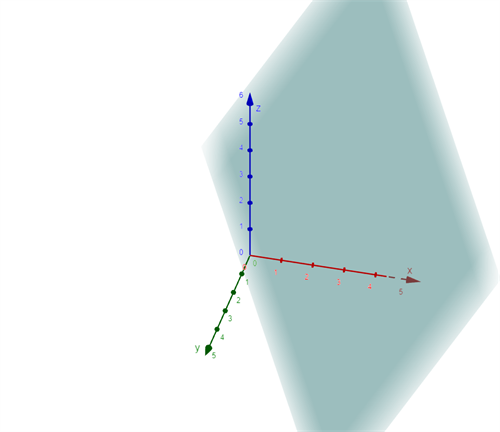
மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாடு \(ax + by + cz + d = 0\) ஆனது தளத்தைக் குறிக்கும்.
நேரிய சமன்பாடு தொகுப்பிற்க்கான தீர்வுகள்
மூன்று மாறிகளில் நேரியல் சமன்பாட்டு தொகுப்பின் பொதுவான வடிவம்:
\(a_1x + b_1y + c_1z + d_1 = 0\)
\(a_2x + b_2y + c_2z + d_2 = 0\)
\(a_3x + b_3y + c_3z + d_3 = 0\)
ஒரேயொரு தீர்வு: மூன்று சமன்பாடுகள் ஒரு தளத்தில் ஒரு பொதுவான புள்ளியில் சந்திக்குமாயின், அப்புள்ளியே அச்சமன்பாட்டுத் தொகுப்பிற்க்கு ஒரே ஒரு தீர்வு மட்டுமே இருக்கும்.
எண்ணிக்கையற்ற தீர்வுகள்: மூன்று சமன்பாடுகள் ஒரே தளத்தின் மேல் சந்திக்குமாயின், அச்சமன்பாட்டுத் தொகுப்பிற்க்கு எண்ணிக்கையற்ற தீர்வுகள் இருக்கும்.
தீர்வு இல்லை: மூன்று சமன்பாடுகளுக்கும் எந்த ஒரு பொதுவான புள்ளியும் இல்லையென்றால், அச்சமன்பாட்டிற்க்கு தீர்வு இருக்காது.
மூன்று மாறிகளில் அமைந்த நேரிய சமன்பாட்டு தொகுப்பிற்க்கு தீர்வு காணும் படிநிலைகள்
படி 1: \(3\) சமன்பாடுகளிலிருந்து ஏதேனும் \(2\) சமன்பாடுகளைக் எடுதுக்கொள்வோம். மற்றும் மாறிகளை விட்டுவிட்டு, ஏதேனும் ஒரு மாறியை ரத்து செய்யும் வகையில் பொருத்தமான மதிப்புகளுடன் சமன்பாடுகளைப் பெருக்கவும். பின்பு சமன்பாடு \(x\) மற்றும் \(y\) அல்லது \(x\) மற்றும் \(z\) அல்லது \(y\) மற்றும் \(z\) ஆகிய ஏதேனும் இரண்டு மாறிகளைக் கொண்டு இருக்கும்.
படி 2: மீண்டும், \(3\) சமன்பாடுகளிலிருந்து ஏதேனும் \(2\) சமன்பாடுகளைக் எடுதுக்கொண்டு, முந்தைய சோடியில் நீக்கப்பட்ட அதே மாறியை நீக்கவும்.
படி 3: இப்போது, இரண்டு மாறிகள் கொண்ட \(2\) சமன்பாடுகள் உள்ளன.
படி 4: இந்த \(2\) சமன்பாடுகளை பிரதியிடல் அல்லது நீக்குதல் அல்லது குறுக்கு பெருக்கல் முறை போன்ற ஏதேனும் ஒரு முறையைப் பயன்படுத்தி தீர்க்கவும்.
படி 5: கொடுக்கப்பட்ட சமன்பாடுகளிள் ஏதேனும் ஒன்றில் இந்த \(2\) மாறிகளின் மதிப்பை பிரதியிட மூன்றாவது மாறியின் மதிப்பை பெறலாம்.
Important!
1. ஏதேனும் ஒரு படிநிலையில், \(0 = 1\) போன்ற தவறான சமன்பாட்டைப் பெற்றால், அந்த சமன்பாட்டுத் தொகுப்பு ஒருங்கமைவற்றது மற்றும் தீர்வு இல்லை.
2. \(0 = 0\) போன்ற சமன்பாட்டைப் பெற்றால், சமன்பாட்டுத் தொகுப்பு ஒருங்கமைவுடையது மற்றும் எண்ணற்ற தீர்வுகளைக் கொண்டிருக்கும்.
Register for free to see more content