PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoநேர் விகிதத்தில், இரண்டு அளவுகள் x மற்றும் y ஆகியவை அந்தந்த மதிப்புகளின் விகிதங்கள் மாறிலி ஆகா( நிலையானதாக) இருக்கும் வகையில் ஒன்றாக அதிகரிக்கும் (அல்லது குறையும்) எனக் கூறப்படுகிறது.
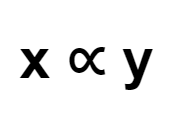
அதாவது, \frac{x}{y} = k நேர்மறையாக இருந்தால், x மற்றும் y நேரடியாக மாறுபடும். அதாவது, x மற்றும் y நோ் விகிதத்தில் உள்ளன.
x மற்றும் y அளவுகள் நோ் விகிதத்தில் இருக்கும் போது, நாம் = என்று எழுதலாம். xன் மதிப்புகளான , க்குத் தொடா்புடைய yன் மதிப்புகள் , ஆகும்.
Example:
உதாரணமாக,
ஒரு சா்க்கரையின் 1 பங்குக்கு 75 \text{மி.லி} தண்ணீா் தேவை என்றால், 1800 \text{மி.லி.} தண்ணீாில் எவ்வளவு சர்க்கரையை கலக்க வேண்டும்?
1800 \text{மி.லி.} x சா்க்கரையின் பாகங்கள் கலப்பதாக இருக்கட்டும்.
நடைமுறையில், ஒரு சா்க்கரையின் 1 பகுதிக்கு 75 \text{மி.லி}, தண்ணீா் தேவைப்பட்டால், 1800 \text{மி.லி.} தண்ணீருக்கு அதிக சா்க்கரை தேவைப்படுகிறது.
நீரின் அளவு அதிகரிப்பதால் சர்க்கரையின் அளவு அதிகரிக்கிறது. எனவே இது நேர் விகிதத்தில் உள்ளது.
x மற்றும் y நோ் விகிதத்தில் இருக்கும் போது, நாம் = என்று எழுதலாம். xன் மதிப்புகளான , க்குத் தொடா்புடைய yன் மதிப்புகள் , ஆகும்.
சூத்திரத்தில் அறியப்பட்ட மதிப்புகளை மாற்றவும்.
\frac{1}{75} = \frac{x}{1800}
75 x = 1 1800
x = \frac{1800}{75}
x = 24
எனவே, 24 பாகங்கள் சா்க்கரையை 1800 \text{மி.லி.} தண்ணீாில் கலக்க வேண்டும்.
Register for free to see more content