PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demo1. முக்கோணத்தின் இரண்டு சாய்ந்த வரிசையும் எப்போதும் ஒன்றுதான்.
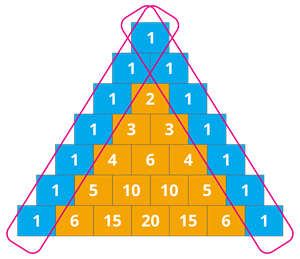
2. முதல் மூலைவிட்டமானது இயல் எண்கள் ஆகும்.
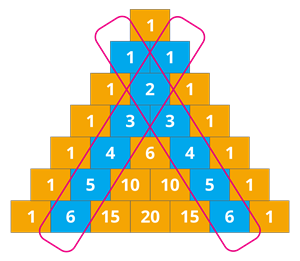
3. இரண்டாவது மூலைவிட்டத்தின் எண்களின் வித்தியாசம் இயல் எண்கள் ஆகும்.
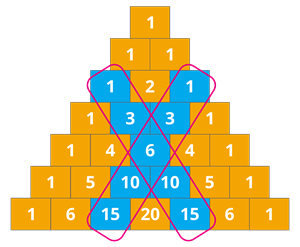
4. இரண்டாவது மூலைவிட்ட எண்கள் முக்கோண எண்கள் ஆகும்.
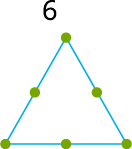
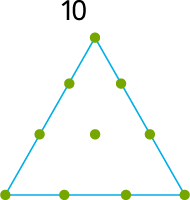
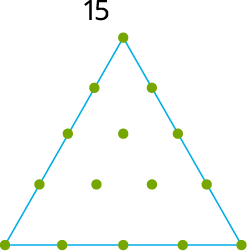
ஒரு முக்கோண எண் என்பது ஒரு சமபக்க முக்கோண புள்ளி வடிவத்தை உருவாக்கக்கூடிய ஒரு எண்ணாகும்.
எடுத்துக்காட்டாக, \(1\), \(3\), \(6\), \(10\) மற்றும் \(15\) ஆகியன முகோண எண்கள்.
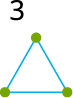
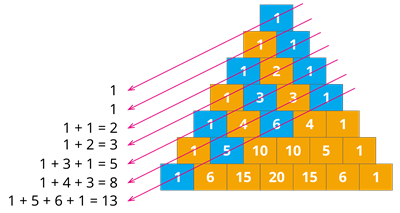
5. பாஸ்கலின் முக்கோணத்தின் சாய்ந்த வரிசைகளில் உள்ள உறுப்புகளின் கூடுதல் ஃபைபோனச்சி வரிசையை அளிக்கிறது.
6. அறுங்கோண வடிவமைப்பு:
பாஸ்கல் முக்கோணத்தின் அறுங்கோணத்தின் ஒன்று விட்ட பக்கங்களின் பெருக்கற்பலன் மற்றொரு ஒன்று விட்ட பக்கங்களின் பெருக்கற்பலனுக்கு சமம்.
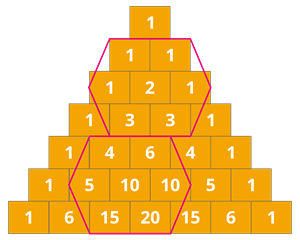
கீழ்கண்ட எடுத்துக்காட்டு மூலம் இதனை காணலாம்.
அறுங்கோணம் | பச்சை நிற ஒன்று விட்ட எண்களின் பெருக்கற்பலன் | பச்சை நிற ஒன்று விட்ட எண்களின் பெருக்கற்பலன் | சமம்/சமம் அல்ல |
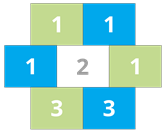 | \(1 \times 1 \times 3 = 3\) | \(1 \times 1 \times 3 = 3\) | சமம் |
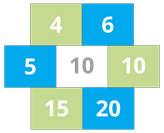 | \(4 \times 10 \times 15 = 600\) | \(6 \times 5 \times 20 = 600\) | சமம் |
Register for free to see more content