PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoசரிவகம்:
ஒரு சோடி எதிர்ப்பக்கங்களை இணையாகக் கொண்ட ஒரு நாற்கரமே சரிவகமாகும்.
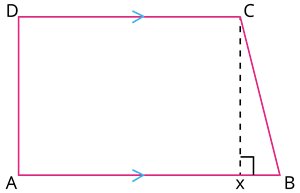
படத்திலிருந்து, \(AB\) மற்றும் \(CD\) ஆகியவை இணைபக்கங்கள் மற்றும் \(AD\) மற்றும் \(BC\) ஆகியவை இணை பக்கங்கள் அல்ல.
Important!
• இணை பக்கங்களுக்கு இடையேயுள்ள தொலைவு சரிவகத்ஹ்டின் உயரம் ஆகும், படத்திலிருந்து, \(CX\) என்பது உயரம் ஆகும்.
• சரிவகத்தின் அனைத்து கோணங்களின் கூடுதல் \(360^{\circ}\) ஆகும்.
இருசமபக்கச் சரிவகம்:
ஒரு சரிவகத்தின் இணையற்ற பக்கங்கள் சமமாகவும்
அடிப்பக்கத்தின் மீது சம அளவுள்ள கோணங்களையும் உருவாக்கினால்,
அது ஓர் இருசமபக்கச் சரிவகம் ஆகும்.
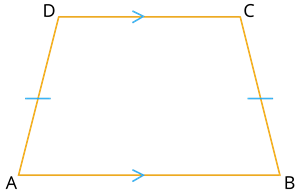
இங்கு, \(AD\) மற்றும் \(BC\) ஆகியன சமம் மற்றும் \(\angle A\) மற்றும் \(\angle B\) ஆகியன சமம்.
சரிவகத்தின் பரப்பளவு:
சரிவகத்தின் பரப்பளவு \(A = \frac{1}{2} \times h \times (a +b)\) சதுர அலகுகள் என்ற சூத்திரத்தைப் பயன்படுத்தி கணக்கிடப்படுகிறது.
இங்கு, \(h\) என்பது சரிவகத்தின் உயரம் ஆகும்.
\(a\) மற்றும் \(b\) என்பன இணைப்பக்கங்களின் நீளம் ஆகும்.
Example:
சரிவகத்தின் உயரம்' \(12\) செ.மீ மற்றும் இணைப்பக்கங்களின் அளவுகள் \(5\) செ.மீ மற்றும் \(6\) செ.மீ எனில் சரிவகத்தின் பரப்பளவு காண்க:
தீர்வு:
கொடுக்கப்பட்டது \(h\) \(=\) \(12\) செ.மீ, \(a\) \(=\) \(5\) செ.மீ மற்றும் \(b\) \(=\) \(6\) செ.மீ.
சரிவகத்தின் பரப்பளவு, \(A\) \(=\) \(\frac{1}{2} \times h \times (a +b)\)
\(=\) \(\frac{1}{2} \times 12 \times (5 + 6)\)
\(=\) \(6 \times 11\)
\(=\) \(66\) செ.மீ \(^2\)
சரிவகம் வரையும் வழிகள்:
கீழே கொடுக்கப்பட்டுள்ள அளவுகளைப் பயன்படுத்தி சரிவகம் வரையும் முறைகளைக் காணலாம்.
1. மூன்று பக்கங்கள் மற்றும் ஒரு மூலைவிட்டம்.
2. மூன்று பக்கங்கள் மற்றும் ஒரு கோணம்.
3. இரு பக்கங்கள் மற்றும் இரு கோணங்கள்.
4. நான்கு பக்கங்கள்.
Register for free to see more content