PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free Demoகணங்களின் வித்தியாசம் (Difference of Two Sets)
கணம் \(A\) மற்றும் கணம் \(B\) இன் வித்தியாசம் என்பது கணம் \(A\) இல் உள்ள, ஆனால் கணம் \(B\) இல் இல்லாத உறுப்புகளைக் கொண்ட கணமாகும். இதை \(A – B\) அல்லது \(A \ B\) என எழுதலாம். \(A – B\) என்பதை \(A\) வித்தியாசம் \(B\) எனப் படிக்க வேண்டும்.
அதாவது, \(A - B = \{ x : x \in A \ \text{மற்றும்} \ x \notin B\}\) மற்றும் \(B - A = \{ x : x \notin A \ \text{மற்றும்}\ x \in B\}\).
\(A - B\) மற்றும் \(B - A\) ஐ உதாரணத்துடன் வென்படத்தைக் கொண்டு காண்போம்.
\(A = \{2, 4, 6, 8\}\) மற்றும் \(B = \{6, 8, 10, 12\}\)
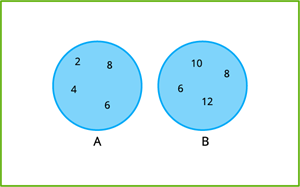
\(A - B = \{2, 4, 6, 8\} - \{6, 8, 10, 12\}\) \(A - B = \{2, 4\}\) |  |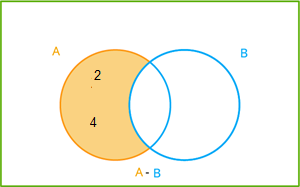
\(B - A = \{6, 8, 10, 12\} - \{2, 4, 6, 8\}\) \(B - A = \{10, 12\}\) |  |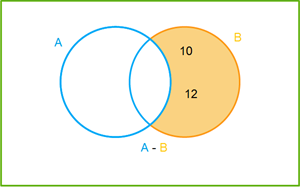
(i) \(A' = U - A\)
(ii) \(A - B = A \cap B'\)
(iii) \(A - A = \phi\)
(iv) \(A - \phi = A\)
(v) \(A - B = B - A \Leftrightarrow A = B\)
(vi) \(A - B = A\) எனில் \(A \cap B = \phi\)
கணங்களின் சமச்சீர் வித்தியாசம் (Symmetric Difference of Sets)
\(A\) மற்றும் \(B\) என்ற கணங்களின் சமச்சீர் வித்தியாசம் என்பது \((A–B)\) மற்றும் \((B–A)\) இவற்றின் சேர்ப்பாகும். இது \(A \Delta B\) எனக் குறிப்பிடப்படுகிறது.
\(A \Delta B = (A - B) \cup (B - A)\)
\(A \Delta B = \{x : x \in A - B \ \text{அல்லது} \ x \in B - A\}\)
\(A - B\) மற்றும் \(B - A\) ஐ உதாரணத்துடன் வென்படத்தைக் கொண்டு காண்போம்.
\(A = \{2, 4, 6, 8\}\) மற்றும் \(B = \{6, 8, 10, 12\}\)
\(A - B = \{2, 4\}\) மற்றும் \(B - A = \{10, 12\}\)
\(A \Delta B = \{2, 4\} \cup \{10, 12\}\)
\(A \Delta B = \{2, 4, 10, 12\}\)
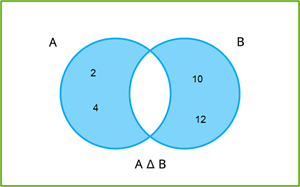
(i) \(A \Delta A = \phi\)
(ii) \(A \Delta B = B \Delta A\)
(iii) \(A \Delta B = \{x : x \in A \cup B \ \text{அல்லது} \ x \notin A \cap B\}\)
(iv) \(A \Delta B = (A \cup B) - (A \cap B)\)
வெட்டாக் கணங்கள் (Disjoint sets)
\(A\) மற்றும் \(B\) ஆகிய இரு கணங்களுக்குப் பொதுவான உறுப்புகள் எதுவும் இல்லை எனில் அவை வெட்டாக்கணங்கள் ஆகும். அதாவது, \(A \cap B = \phi\) எனில், \(A\) மற்றும் \(B\) வெட்டாக் கணங்கள் ஆகும்.
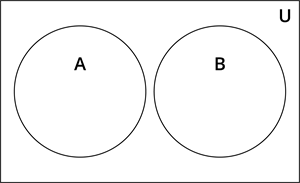
\(A = \{a, e, i, o, u\}\) மற்றும் \(B = \{b, c, d, f, g\}\)
\(A \cap B = \{a, e, i, o, u\} \cap \{b, c, d, f, g\}\)
\(A \cap B = \phi\)
\(A\) மற்றும் \(B\) இல் எந்த உறுப்புகளும் பொதுவான உறுப்புகள் இல்லை. எனவே, இவை வெட்டாக் கணங்கள் ஆகும்.
Important!
\(A \cup B \ne \phi\) எனில், \(A\) மற்றும் \(B\)ஆகியவை வெட்டும் கணங்கள் (Overlapping) எனப்படும். அதாவது, இரு கணங்களுக்கு இடையே குறைந்தபட்சம் ஒரு பொது உறுப்பாவது இருந்தால் அவை வெட்டும் கணங்கள் ஆகும்.
Register for free to see more content