PDF chapter test TRY NOW
கணங்களின் சேர்ப்பு (Union of Two Sets)
A மற்றும் B இன் சேர்ப்புக் கணம் என்பது இரு கணங்களிலும் உள்ள அனைத்து உறுப்புகளையும் கொண்ட கணம் ஆகும். இரு கணத்திற்கும் பொதுவான உறுப்புகளை ஒரு முறை மட்டும் கணக்கில் கொள்ள வேண்டும். சேர்ப்புக் கணத்தைக் குறிக்க \cup குறியீடாகப் பயன்படுத்தப்படுகிறது. A \cup B இதனை A சேர்ப்பு B எனப் படிக்க வேண்டும்.
அதாவது, A \cup B = \{x : x \in A \text{அல்லது} x \in B\}.
A \cup B ஐ உதாரணத்துடன் வென்படத்தைக் கொண்டு காண்போம்.
A = \{2, 4, 6, 8\} மற்றும் B = \{6, 8, 10, 12\}
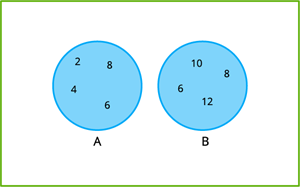
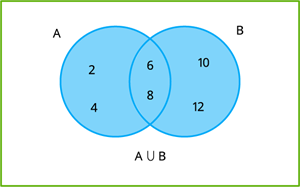
A \cup B = \{2, 4, 6, 8\} \cup \{6, 8, 10, 12\}
A \cup B = \{2, 4, 6, 8, 10, 12\}
இங்கு, 6 மற்றும் 8 ஆகிய உறுப்புகள் இரண்டு கணங்களிலும் வருவதால் அதை ஒருமுறை மட்டுமே கணக்கிட வேண்டும்.
கணங்களில் வெட்டு (Intersection of Two Sets)
A மற்றும் B இன் வெட்டுக் கணம் என்பது இரு கணங்களிலும் உள்ள பொதுவான உறுப்புகளைக் கொண்ட கணம் ஆகும். வெட்டுக் கணத்தைக் குறிக்க \cap குறியீடாகப் பயன்படுத்தப்படுகிறது. A \cap B இதனை A வெட்டு B எனப் படிக்க வேண்டும்.
அதாவது, A \cap B = \{x : x \in A \text{மற்றும்} x \in B\}.
A \cap B ஐ உதாரணத்துடன் வென்படத்தைக் கொண்டு காண்போம்.
A = \{2, 4, 6, 8\} மற்றும் B = \{6, 8, 10, 12\}
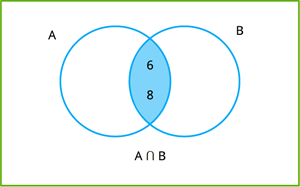
A \cap B = \{2, 4, 6, 8\} \cap \{6, 8, 10, 12\}
A \cap B = \{6, 8\}
இங்கு, 6 மற்றும் 8 ஆகிய உறுப்புகள் மட்டுமே இரண்டு கணங்களிலும் வருவதால் அதுவே பொதுவான உறுப்புகள் ஆகும்.
Important!
(i) A \cup A = A \cap A = A
(ii) A \cup \phi = A மற்றும் A \cap \phi = \phi
(iii) A \cup U = U மற்றும் A \cap U = A
(iv) A \subseteq A \cup B \subseteq மற்றும் B \subseteq A \cup B
(v) A \cap B \subseteq A மற்றும் A \cap B \subseteq B
(vi) A \cup B = B \cup A மற்றும் A \cap B = B \cap A
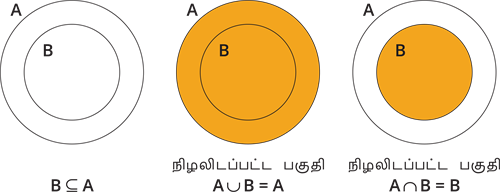
(viii) A \cup B = A \cap B எனில், A = B.
Register for free to see more content