PDF chapter test TRY NOW
சர்வசம முக்கோணங்கள் : ஒரு முக்கோணத்தின் அனைத்துப் பக்கங்களும், கோணங்களும் மற்றொரு முக்கோணத்தின் ஒத்த பக்கங்களுக்கும், ஒத்த கோணங்களுக்கும் சமமானால் அவ்விரு முக்கோணங்கள்
சர்வசம முக்கோணங்கள் எனப்படும்.
சர்வசம முக்கோணங்கள் எனப்படும்.
மேற்கண்ட படத்தில் இருந்து,Δ ABC மற்றும் Δ DEF ஒரே அளவு மற்றும் உருவமும் கொண்டவை. எனவே அவை சர்வசமம். Δ ABC ≅ Δ DEF எனக் குறிப்பிடலாம் .
மேலும், A யின் மீது D, B யின் மீது E யின் மீது C யின் மீது F, சரியாக பொருந்துகிறது.
எனவே, கீழ்கண்டவற்றை காண்போம்:
Important!
தொடர்புடைய முனைகள்: A மற்றும் D, B மற்றும் E, மற்றும் C மற்றும் F.
தொடர்புடைய பக்கங்கள்: AB மற்றும் DE, BC மற்றும் EF, மற்றும் CA மற்றும் FD.
தொடர்புடைய கோணங்கள்: ∠A மற்றும் ∠D, ∠B மற்றும் ∠E, மற்றும் ∠Cமற்றும் ∠F.
தொடர்புடைய பக்கங்கள்: AB மற்றும் DE, BC மற்றும் EF, மற்றும் CA மற்றும் FD.
தொடர்புடைய கோணங்கள்: ∠A மற்றும் ∠D, ∠B மற்றும் ∠E, மற்றும் ∠Cமற்றும் ∠F.
பல்வேறு வகையான சர்வசம முக்கோணங்கள் பற்றி காண்போம்:
- ப-ப-ப சர்வசமம்
- கோ -ப-கோ சர்வசமம்
- செ-க-ப சர்வசமம்
ப -ப -ப சர்வசமம் : ஒரு முக்கோணத்தின் மூன்று பக்கங்களும் மற்றொரு முக்கோணத்தின் மூன்று பக்கங்களுக்கு இணையாக இருக்கும்.
ப-ப-ப என்பதன் விரிவாக்கம் "பக்கம் பக்கம் பக்கம் " இரு முக்கோணத்தின் மூன்று பக்கங்களும் சமம் எனில் அவை ப-ப-ப சர்வசம முக்கோணங்கள்.
Example:
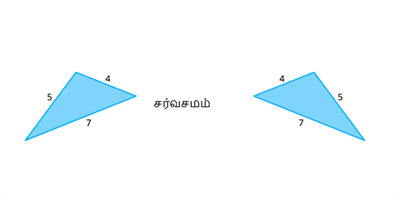
ஒரு முக்கோணத்தின் மூன்று பக்க அளவுகள் 4 அலகுகள், 5 அலகுகள் மற்றும் 7 அலகுகள்
மற்றொரு முக்கோணத்தின் மூன்று பக்க அளவுகள்4 அலகுகள், 5 அலகுகள் and 7 அலகுகள் இரண்டும் சமமாக இருப்பதால் இவை ப-ப-ப சர்வசம முக்கோணங்கள்.
ப -கோ -ப சர்வசமம் : ஒரு முக்கோணத்தின் ஒரு பக்கம் மற்றும் கோணமானது மற்றொரு முக்கோணத்தின் ஒரு பக்கம் மற்றும் கோணத்திற்கு சமம் எனில் அவை ப -கோ -ப சர்வசமம்.
Example:
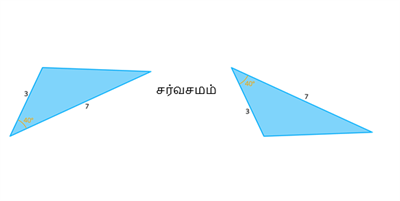
ஒரு முக்கோணத்தின் இரு பக்க அளவுகள் 3 அலகுகள் மற்றும் 7 அலகுகள்,மற்றும் கோணஅளவு 40° இது மற்றொரு முக்கோணத்தின் இரு பக்க அளவுகள் (3\) அலகுகள் மற்றும் 7 அலகுகள் உடன் கோணஅளவு 40° க்கு சமம். எனவே, இவை ப -கோ -ப சர்வசம முக்கோணங்கள்.
Important!
ப -கோ -ப என்பதன் விரிவாக்கம் "பக்கம் கோணம் பக்கம்" முக்கோணத்தின் இரு பக்கம் மாற்றுன ஒரு கோணம் சமமாக இருக்கும்.
கோ -ப -கோ சர்வசமம் : ஒரு முக்கோணத்தின் இரு கோணங்கள் மற்றும் ஒரு பக்க அளவானது மற்றொரு முக்கோணத்தின் இரு கோணங்கள் மற்றும் ஒரு பக்க அளவிற்கு சமம் எனில் அவை கோ -ப கோ சர்வசம முக்கோணம்.
Example:
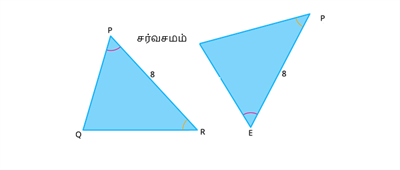
ஒரு முக்கோணத்தின் இரு கோணங்கள் 40° மற்றும் 60° அலகுகள், மற்றும் பக்க அளவு 8 ஆகுகள் மற்றொரு முக்கோணத்தின் இரு கோண அளவுகள் 40° மற்றும் 60° பக்க அளவுகள் 8 அலகுகளுக்கு சமம் எனில் அவை கோ -ப - கோ சர்வசம முக்கோணம்.
Important!
கோ -ப - கோ என்பதன் விரிவாக்கம் "கோணம் பக்கம் கோணம் " ஒரு முக்கோணத்தின் இரு கோணங்கள் மற்றும் ஒரு பக்க அளவானது மற்றொரு முக்கோணத்தின் இரு கோண மற்றும் ஒரு பக்க அளவிற்கு சமம்.
Register for free to see more content