PDF chapter test TRY NOW
சமமான நாண்களின் பண்புகள்:
O வை மையமாக கொண்ட வட்டம் மற்றும் இரு சம நாண்கள் PQ மற்றும் RS.
PQ மற்றும் RS என்ற நாணின் முனைகள் Q மற்றும் R இணைக்க.
கோடு OA ஆனது RS மற்றும் OB செங்குத்து PQ க்கும் செங்குத்தாகும்.
இரு செங்கோண முக்கோணங்கள் OAR மற்றும் OBQ உடன் \angle OAR = \angle OBQ = 90^{\circ} எனவே OA \perp RS மற்றும் OB \perp PQ.
இங்கு, OP மற்றும் OQ என்பன ஆரங்கள். அவை சமம்.
தேற்றத்தின் படி, வட்டத்தின் மையத்தில் செங்குத்து மற்றும் நாண்ணை இரு சமகூரிடும். ஆகவே, RA = BQ நாண்கள் சமம்.
எனவே, விதியின் படி, முக்கோணங்கள் சர்வசமம்.
பக்கங்கள் OA = OB.
இதிலிருந்து பின்வரும் முடிவைப் பெறுகின்றோம்.
தேற்றம்: வட்டத்தில் உள்ள சம நாண்கள் மையத்தில் இருந்து சம தொலைவில் இருக்கும்.
விளக்கம்:
தேற்றத்தின் படி, இரு நாண்கள் PQ மற்றும் RS என்பன சமம், நாண்களுக்கு இடைப்பட்ட தொலைவு PQ மற்றும் RS மையம் O வில் இருந்து சமம் .
O\text{வில் இருந்து}PQ\text{என்ற நாண்னிற்கு உள்ள தொலைவு} = O\text {வில் இருந்து}\(RS\text{என்ற நாண்னிற்கு உள்ள தொலைவு}\).
Example:
வட்டத்தில் சம மற்றும் இணையான நாண்கள் உள்ளது. ஒரு நாண் மையத்தில் இருந்து 5 செ. மீ தொலைவில் உள்ளது, இரு நாண்களுக்கு இடைப்பட்ட தொலைவைக் காண்க.
விடை:
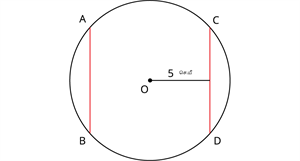
O வை மையாகமாகவும் மற்றும் AB மற்றும் CD சமமான நாண்கள் கொண்ட வட்டமாகும்.
ஒரு நாண் மையத்தில் இருந்து 5 செ. மீ தொலைவில் உள்ளது.
நாண் CD மையத்தில் இருந்து 5 செ. மீ தொலைவில் உள்ளது.
தேற்றத்தில் இருந்து, நாண்கள் AB மற்றும் CD வட்டத்தின் மையத்தில் இருந்து சம தொலைவில் உள்ளது.
நாண் AB மற்றும் மையம் O வில் இருந்து 5 செ. மீ.
இரு நாண்களுக்கு இடைப்பட்ட தொலைவு:
= 5 செ.மீ + 5 செ.மீ
= 10 செ.மீ
தேற்றத்தின் மறுதலை :வட்ட மையத்திலிருந்து சம தொலைவில் உள்ள நாண்கள் சம
நீளமுள்ளவை .
விளக்கம்:
தேற்றத்தின் படி, இரு நாண்கள் PQ மற்றும் RS மையம் O வில் இருந்து சம தொலைவிலும், நாண்கள் PQ மற்றும் RS சமம் . (i.e.) PQ = RS.
Example:
இரு நாண்கள் இணைந்து ஒரு கோட்டுத்துண்டு உருவாகிறது அக்கோட்டுத்துண்டு வட்டத்தின் மையத்தின் வழியாக செல்கிறது எனில், நாண்கள் சம நீளம் உடையவை என நிரூபிக்க.
விடை :
இரு நாண்கள் இணைந்து ஒரு கோட்டுத்துண்டு உருவாகிறது அக்கோட்டுத்துண்டு வட்டத்தின் மையத்தின் வழியாக செல்கிறது
நாண்கள் வட்ட மையத்தில் இருந்து சம தொலைவில் இருக்கும்.
தேற்றத்தின் படி, நாண்கள் சம நீளம் உடையவை.
நிரூபிக்கப்பட்டது.
Register for free to see more content