PDF chapter test TRY NOW
\(x\)-ஆயஅச்சிலுள்ள புள்ளி:
\(x\)-ஆயஅச்சிலுள்ள புள்ளி என்பது \(x\)-அச்சில் அளவிடப்படும் \(y\)-அச்சிற்கு செங்குத்து தொலைவிலுள்ள தூரம் ஆகும்.
\(y\)-ஆயஅச்சிலுள்ள புள்ளி:
\(y\)-ஆயஅச்சிலுள்ள புள்ளி என்பது \(y\)-அச்சில் அளவிடப்படும் \(x\)-அச்சிற்கு செங்குத்து தொலைவிலுள்ள தூரம் ஆகும்.
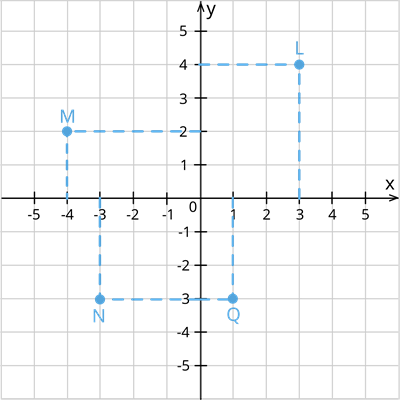
1. \(y\)-அச்சிலிருந்து \(L\) என்ற புள்ளியின் செங்குத்து தூரமானது \(y\)-அச்சின் நேர் திசையில் \(LX=4\) அலகுகள் மற்றும் \(x\)-அச்சிலிருந்து \(L\) என்ற புள்ளியின் செங்குத்து தூரமானது \(x\)-அச்சின் நேர் திசையில் \(OL=3\) அலகுகள் ஆகும்.
கொடுக்கப்பட்டுள்ள வரைபடத்தில் புள்ளி \(L\) ஆனது முதல் காற்பகுதியில் அமைகிறது, இதை \((x, y)\) என குறிப்பிடலாம். இங்கு \(x=3\) மற்றும் \(y=4\) எனவே கார்டீசியன் தளத்தில் புள்ளி \(L\) ஆனது \((3,4)\) என குறிப்பிடப்படுகிறது.
2. \(y\)-அச்சிலிருந்து \(M\) என்ற புள்ளியின் செங்குத்து தூரமானது \(y\)-அச்சின் நேர் திசையில் \(MX'=2\) அலகுகள் மற்றும் \(x\)-அச்சிலிருந்து \(M\) என்ற புள்ளியின் செங்குத்து தூரமானது \(x\)-அச்சின் எதிர் திசையில் \(OM=2\) அலகுகள் ஆகும்.
கொடுக்கப்பட்டுள்ள வரைபடத்தில் புள்ளி \(M\) ஆனது இரண்டாம் காற்பகுதியில் அமைகிறது, இதை \((-x, y)\) என குறிப்பிடலாம். இங்கு \(x=4\) மற்றும் \(y=2\) எனவே கார்டீசியன் தளத்தில் புள்ளி \(M\) ஆனது \((-4,2)\) என குறிப்பிடப்படுகிறது.
கொடுக்கப்பட்டுள்ள வரைபடத்தில் புள்ளி \(N\) ஆனது மூன்றாம் காற்பகுதியில் அமைகிறது, இதை \((-x, -y)\) என குறிப்பிடலாம். இங்கு \(x=2\) மற்றும் \(y=3\) எனவே கார்டீசியன் தளத்தில் புள்ளி \(N\) ஆனது \((-2,-3)\) என குறிப்பிடப்படுகிறது.
4. \(y\)-அச்சிலிருந்து \(Q\) என்ற புள்ளியின் செங்குத்து தூரமானது \(y\)-அச்சின் எதிர் திசையில் \(QX=3\) அலகுகள் மற்றும் \(x\)-அச்சிலிருந்து \(Q\) என்ற புள்ளியின் செங்குத்து தூரமானது \(x\)-அச்சின் நேர் திசையில் \(OX = 1\) அலகுகள் ஆகும்.
கொடுக்கப்பட்டுள்ள வரைபடத்தில் புள்ளி \(Q\) ஆனது நான்காம் காற்பகுதியில் அமைகிறது, இதை \((x, -y)\) என குறிப்பிடலாம். இங்கு \(x=1\) மற்றும் \(y=3\) எனவே கார்டீசியன் தளத்தில் புள்ளி \(Q\) ஆனது \((1,-3)\) என குறிப்பிடப்படுகிறது.
Important!
நேர்மறை ஆயத்தொலைவின் மதிப்பை நேர் திசையிலும் எதிர்மறை ஆயத்தொலைவின் மதிப்பை எதிர் திசையிலும் அளவிடலாம்.
Register for free to see more content