2. Distance formula

Let us consider an example to understand the concept.

 

Priya wants to go shopping. She started from her home \(A\) and travelled \(3 \ kms\) east and then, travelled \(4 \ kms\) north. Now, let us draw a diagrammatic representation of this scenario.

 

 

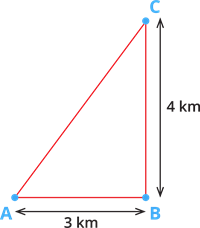
Now, how will you find the distance between the points \(A\) and \(C\)?

 

Obviously, from the figure, we can say that by applying the Pythagorean theorem, we can find the distance between the points \(A\) and \(C\).

 

That is \(AC = \sqrt{AB^2 + BC^2}\)

 

\(AC = \sqrt{3^2 + 4^2}\)

 

\(AC = 5 \ km\)

 

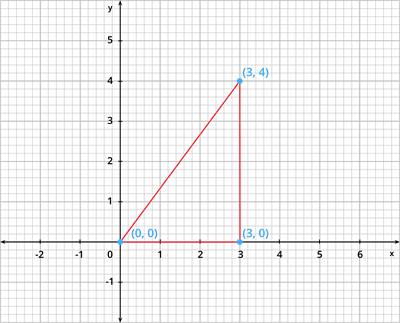
Suppose, if the points lie on the \(x\) - axis. Say for points \(A(0,0)\) and \(B(0,3)\). Then, the distance between the points \(A\) and \(B\) is \(AB = 3 - 0 = 3\).

 

 

Similarly, if the points lie on the \(y\) - axis, say for points \(C(0,1)\) and \(D(0,3)\). Then, the distance between \(C\) and \(D\) is \(CD = 3 - 1 = 2\)

 

 

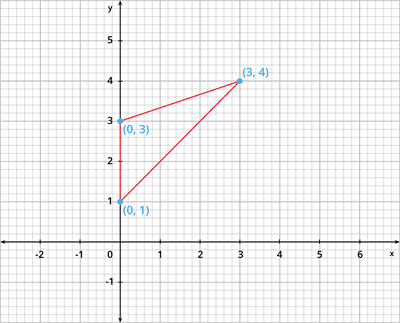
Consider if the points are not on the coordinate axes. Say, for example, \(A(2,3)\) and \(B(3,4)\). Can you determine the distance between these two points.

 

Yes, we can find the distance using the Pythagorean theorem. Let us draw \(AP\) and \(BQ\) perpendicular to the \(x\) - axis. Also, draw \(AC\) perpendicular to \(BQ\). Now, the coordinates of \(P\) and \(Q\) are \((2,0)\) and \((3,0)\), respectively. Then, \(PA = QC = 3 \ units\), \(PQ = AC = 1 \ unit\) and \(BC = BQ - CQ = 4 - 3 = 1 \ unit\).

 

 

Now, by Pythagorean theorem, we have:

 

\(AB^2 = AC^2 + CB^2\)

 

\(AB^2 = 1^2 + 1^2\)

 

\(AB^2 = 2\)

 

\(AB = \sqrt{2}\)

Consider any two points \(P(x_1,y_1)\) and \(P(x_2,y_2)\). Draw \(PR\) perpendicular to \(OS\). Draw \(PT\) perpendicular to \(QS\). Then, \(OR = x_1\), \(OS = x_2\), \(RS = OS - OR = x_2 - x_1 = PT\)

 

\(SQ = y_2\), \(ST = PR = y_1\), \(QT = y_2 - y_1\)

 

Applying Pythagorean theorem, we have:

 

\(PQ^2 = PT^2 + TQ^2\)

 

\(PQ^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2\)

 

\(PQ = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)

 

Therefore, the distance between any two points can be determined using the formula \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).