UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreIn grade \(9\), we learnt the basic concepts of the coordinate geometry such as plotting the points in a plane, locating a point in a plane, and the coordinate axes. Let us recall them.
The distance of a point from \(y\) - axis is called as \(x\) - coordinate or the abscissa. The distance of a point from \(x\) - axis is called as \(y\) - coordinate or the ordinate. The points on the \(x\) - axis is of the form \((x,0)\) and the points on the \(y\) - axis is of the form \((0,y)\).
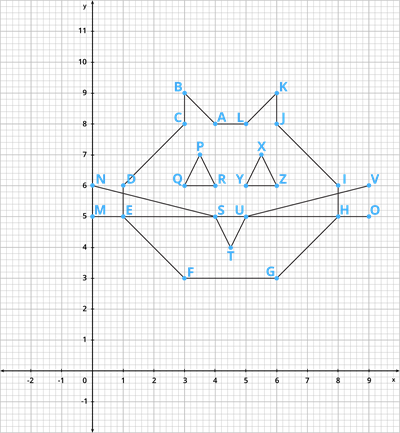
Let us plot the points in the cartesian plane. Join the point \(A(4, 8)\) to \(B(3, 9)\) to \(C(3, 8)\) to \(D(1, 6)\) to \(E(1, 5)\) to \(F(3, 3)\) to \(G(6, 3)\) to \(H(8, 5)\) to \(I(8, 6)\) to \(J(6, 8)\) to \(K(6, 9)\) to \(L(5, 8)\) to \(A\). Also, join the points \(P(3.5, 7)\), \(Q (3, 6)\) and \(R(4, 6)\) to form a triangle. And, \(X(5.5, 7)\), \(Y(5, 6)\) and \(Z(6, 6)\) to form a triangle. Now, join \(S(4, 5)\), \(T(4.5, 4)\) and \(U(5, 5)\) to form a triangle. Lastly, join \(S\) to the points \(M(0, 5)\) and \(N(0, 6)\) and join \(U\) to the points \(O(9, 5)\) and \(V(9, 6)\).
Thus, we get a figure in the shape of a cat's face.
Coordinate Geometry helps us to interpret algebraic results geometrically and serves as a bridge between algebra and geometry. Because of its wide applications, it is used in various fields like engineering, physics, art, etc.
In this chapter, we will learn about the distance between the two points and to find the area of the triangle whose three coordinates are given and the coordinates of the point which divides the line segment into given ratio.
Register for free to see more content