PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA polynomial of the form \(ax + b\), \(a \neq 0\) is a linear polynomial.
The graph of a linear polynomial is a straight line.
Consider the graph of \(y = 2x + 1\).
\(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
\(2x + 1\) | \(2(-2) + 1\) \(=\) \(- 4 + 1\) \(=\) \(-3\) | \(2(-1) + 1\) \(=\) \(- 2 + 1\) \(=\) \(-1\) | \(2(0) + 1\) \(=\) \(0 + 1\) \(=\) \(1\) | \(2(1) + 1\) \(=\) \(2 + 1\) \(=\) \(3\) | \(2(2) + 1\) \(=\) \(4 + 1\) \(=\) \(5\) |
\(y\) \(=\) \(2x + 1\) | \(-3\) | \(-1\) | \(1\) | \(3\) | \(5\) |
Join the coordinates \((-2, -3)\), \((-1, -1)\), \((0, 1)\), \((1, 3)\) and \((2, 5)\) by a straight line so as to obtain the graph of \(y = 2x + 1\).
 |
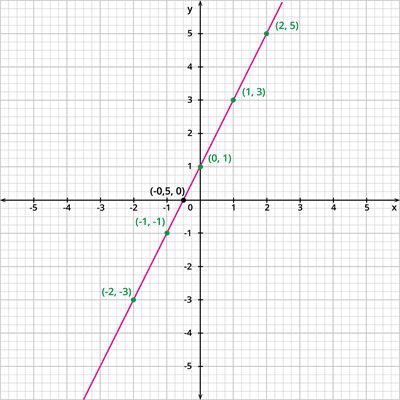It is observed that, the graph of the polynomial \(y = 2x + 1\) intersects the \(x\) \(-\) axis at the point \((- 0.5, 1)\).
Also by the definition, the zero of \(y = 2x + 1\) is given by \(x = \frac{-1}{2} = -0.5\).
Thus, we can say that the zero of a linear polynomial is the \(x\) \(-\) coordinate of the point where the graph of the polynomial intersects the \(x\) \(-\) axis.
In general, for a linear polynomial \(ax + b\), \(a \neq 0\), the graph of \(y = ax + b\) represents a straight line which intersects the \(x\) \(-\) axis exactly at the point \(\left(\frac{-b}{a}, 0\right)\).
The linear polynomial \(ax + b\), \(a \neq 0\), has exactly one zero namely \(\frac{-b}{a}\) which is the \(x\) \(-\) coordinate of the point where the graph of the polynomial intersects the \(x\) \(-\) axis.
Register for free to see more content