PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA polynomial of the form \(ax^2 + bx + c\), \(a \neq 0\) is a quadratic polynomial.
The graph of a quadratic polynomial is a parabolic curve either open upwards or open downwards depending on whether \(a > 0\) or \(a < 0\).
Consider the graph of \(y = 2x^2 + 3x + 1\).
\(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
\(2x^2\) | \(2(-2)^2\) \(=\) \(2(4)\) \(=\) \(8\) | \(2(-1)^2\) \(=\) \(2(1)\) \(=\) \(2\) | \(2(0)^2\) \(=\) \(2(0)\) \(=\) \(0\) | \(2(1)^2\) \(=\) \(2(1)\) \(=\) \(2\) | \(2(2)^2\) \(=\) \(2(4)\) \(=\) \(8\) |
\(3x\) | \(3 \times -2\) \(=\) \(-6\) | \(3 \times -1\) \(=\) \(-3\) | \(3 \times 0\) \(=\) \(0\) | \(3 \times 1\) \(=\) \(3\) | \(3 \times 2\) \(=\) \(6\) |
\(2x^2 + 3x + 1\) | \(8\) \(-\) \(6\) \(+\) \(1\) \(=\) \(3\) | \(2\) \(-\) \(3\) \(+\) \(1\) \(=\) \(0\) | \(0\) \(+\) \(0\) \(+\) \(1\) \(=\) \(1\) | \(2\) \(+\) \(3\) \(+\) \(1\) \(=\) \(6\) | \(8\) \(+\) \(6\) \(+\) \(1\) \(=\) \(15\) |
\(y\) \(=\) \(2x^2 + 3x + 1\) | \(3\) | \(0\) | \(1\) | \(6\) | \(15\) |
Join the coordinates \((-2, 3)\), \((-1, 0)\), \((0, 1)\), \((1, 6)\) and \((2, 15)\) by a smooth curve so as to obtain the graph of \(y = 2x^2 + 3x + 1\).
 |
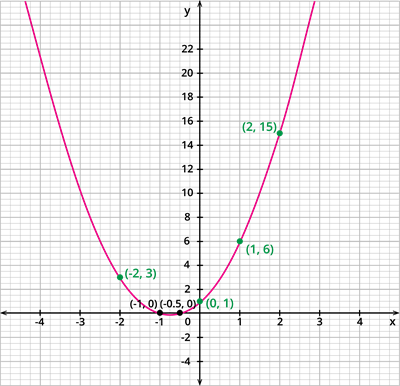It is observed that, the graph of the polynomial \(y = 2x^2 + 3x + 1\) intersects the \(x\) \(-\) axis at the points \((-1, 0)\) and \((-0.5, 0)\).
Thus, we can say that the zero of a quadratic polynomial is the \(x\) \(-\) coordinates of the point where the graph of the polynomial intersects the \(x\) \(-\) axis.
Let us discuss few cases of graphs of a quadratic polynomial.
Case 1: The graph of the quadratic polynomial cuts the \(x\) \(-\) axis at two points, as shown below.
 |  |
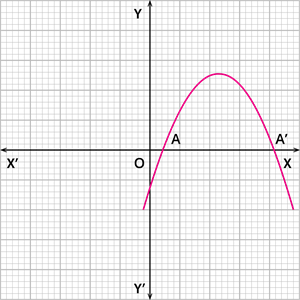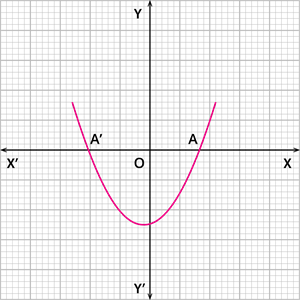In this case, the number of zeroes of the polynomial is \(2\).
Case 2: The graph of the quadratic polynomial cuts the \(x\) \(-\) axis at one point, as shown below.
 |  |
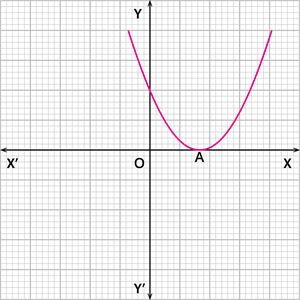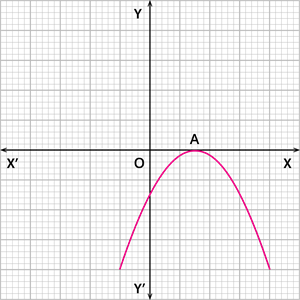In this case, the number of zeroes of the polynomial is \(1\).
Case 3: The graph of the quadratic polynomial does not intersect the \(x\) \(-\) axis at any point, as shown below.
 |  |
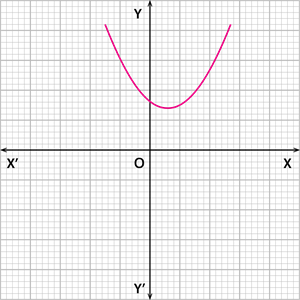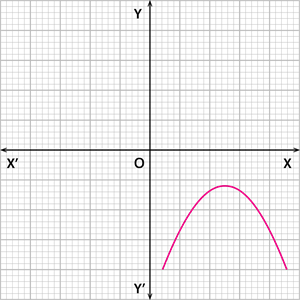In this case, the number of zeroes of the polynomial is \(0\).
The quadratic polynomial \(ax^2 + bx + c\), \(a \neq 0\), has at most two zeroes which is the \(x\) \(-\) coordinates of the point where the graph of the polynomial intersects the \(x\) \(-\) axis.
Register for free to see more content