PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoVariable:
A variable is a symbol that is undefined yet. A variable is something that keeps varying.
If '\(x\)' is a variable, \(x\) can hold the value of any number.
Example:
If '\(x\)' denotes the age of a person, then \(x\) can hold any value from \(1, 2, 3...\) as age cannot be a negative number.
Co-efficient:
A co-efficient is a number used to multiply a variable.
The number multiplied read as being a co-efficient of a variable.
Example:
In \(5p\), \(5\) is the coefficient of '\(p\)'.
Constant:
A constant is any whole number such as \(0, 1, 2, 3,...\)
Expression:
We would have come across many expressions in mathematics such as \(3 + 2\), \(6 - 4\) and so on.
In algebra, such expressions are written using symbols.
An expression is a combination of variables and constants.
An algebraic expression can be both a combination of variables and constants or wholly variables.
Example:
\(2x\) \(+\) \(3\), \(3x\) \(+\) \(4y\) and so on.
Let us look at a few more expressions:
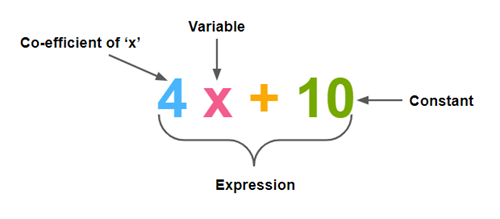
1. Consider \(4x + 10\):
\(4\) is the co-efficient of '\(x\)'.
\(x\) is the variable.
\(10\) is the constant.
\(4x + 10\) is altogether an expression.
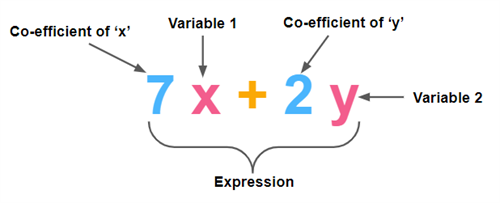
2. Consider \(7x + 2y\).
\(7\) is the co-efficient of '\(x\)'.
\(2\) is the co-efficient of '\(y\)'.
'\(x\)' and '\(y\)' are variable \(1\) and variable \(2\) respectively.
\(7x + 2y\) is altogether an expression.
Register for free to see more content