PDF chapter test TRY NOW
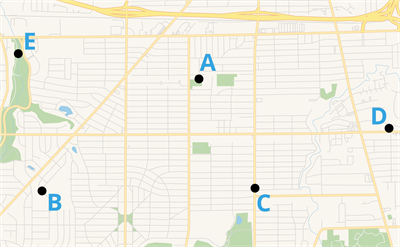
Point
A specific position or location on the surface of the plane is referred to as a point. It has no length, breadth or thickness.
The above figure shows point \(A\) and \(B\).
A point is an invisible dot that may determine a location/position but can't be extended. To represent the location/position, we label each point using an English alphabet.
Example:
We plan to locate the five-place (let them be \(A\), \(B\), \(C\), \(D\) and \(E\)) on a map using the concept of points and label them accordingly.
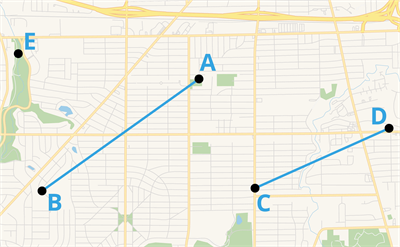
Line segment
A line segment is the shortest distance between two points. It is also a part of the line. Name the line segment using its two endpoints.
Example:
We plan to use the idea of a line segment to illustrate the distance between the places (let's call them \(A\), \(B\), \(C\) and \(D\)) on a map and label them accordingly.
When we connect points \(A\) and \(B\), we get the line segment \(\overline {AB}\).
Also, if we connect the points \(C\) and \(D\), we get the line segment \(\overline {CD}\).
We can calculate the distance of \(\overline {AB}\) and \(\overline {CD}\) using measurements.
Register for free to see more content