PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoLet us discuss what supplementary angles are.
Definition:
When the sum of the two angles is \(180^{\circ}\), the angles are said to be supplementary angles.
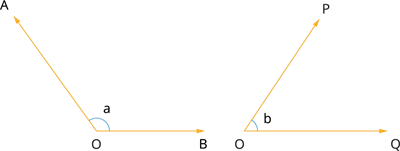
In the figure, \(\angle AOB\) and \(\angle POQ\) is a pair of angles.
The angles \(AOB\) and \(POQ\) are said to be supplementary if \(\angle AOB + \angle POQ = 180^{\circ}\).
Example:
Verify if the given pair of angles are supplementary.
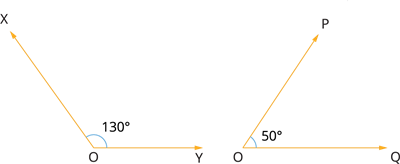
Solution:
Given:
\(\angle XOY\) \(=\) \(130^{\circ}\)
\(\angle POQ\) \(=\) \(50^{\circ}\)
To verify:
Whether the given two angles are supplementary.
Verification:
Add the given two angles.
\(\angle XOY\) \(+\) \(\angle POQ\) \(=\) \(130^{\circ}\) \(+\) \(50^{\circ}\)
\(=\) \(180^{\circ}\)
Since the sum of the two angles is \(180^{\circ}\), by definition, the pair of angles \(XOY\) and \(POQ\) are supplementary.
Important!
When two angles are supplementary, each angle is said to be the supplement of the other.
Here \(\angle XOY\) is the supplement of \(\angle POQ\) and vice versa.
In other words, \(130^{\circ}\) angle is the supplement of \(50^{\circ}\) angle and vice versa.
Register for free to see more content