UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreThe pair of angles are classified into the following based on their relationship with each other.
- Complementary angles
- Supplementary angles
- Adjacent angles
- Linear pair of angles and
- Vertically opposite angles
Let us discuss what complementary angles are.
Definition:
When the sum of the two angles is \(90^{\circ}\), then the angles are called complementary angles.
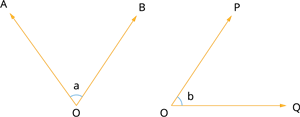
In the figure, \(\angle AOB\) and \(\amgle POQ\) is a pair of angles.
The angles \(AOB\) and \(POQ\) are said to be complementary if \(\angle AOB + \angle POQ = 90^{\circ}\).
Example:
Verify if the given pair of angles are complementary.
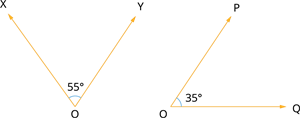
Solution:
Given:
\(\angle XOY\) \(=\) \(55^{\circ}\)
\(\angle POQ\) \(=\) \(35^{\circ}\)
To verify:
Whether the given two angles are complementary.
Verification:
Add the given two angles.
\(\angle XOY\) \(+\) \(\angle POQ\) \(=\) \(55^{\circ}\) \(+\) \(35^{\circ}\)
\(=\) \(90^{\circ}\)
Since the sum of the two angles is \(90^{\circ}\), by definition, the pair of angles \(XOY\) and \(POQ\) are complementary.
Important!
When two angles are complementary, each angle is said to be the complement of the other.
Here \(\angle XOY\) is the complement of \(\angle POQ\) and vice versa.
In other words, \(55^{\circ}\) angle is the complement of \(35^{\circ}\) angle.
Register for free to see more content