
PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoDo you know what the distance of the Sun from the centre of our Galaxy is?
That is, \(300,000,000,000,000,000,000\ m\).
Wow! It's really too long, right? and it is not easy to read it as well.
So, we can simplify it by making this number in standard form, which is much easier to read.
Some values are like the above; it is not easy to read it like the mass of the Sun or the earth's mass. But if we make it into the standard form, we can easily understand it.
In the previous class, you learned to convert the large number to the standard form.
Let's recall that method now.
Wow! It's really too long, right? and it is not easy to read it as well.
So, we can simplify it by making this number in standard form, which is much easier to read.
Some values are like the above; it is not easy to read it like the mass of the Sun or the earth's mass. But if we make it into the standard form, we can easily understand it.
In the previous class, you learned to convert the large number to the standard form.
Let's recall that method now.
Consider a number ; we can rewrite this number in standard form.
That is .
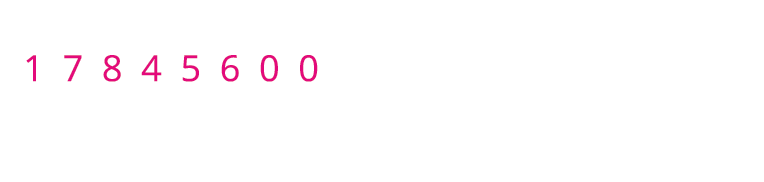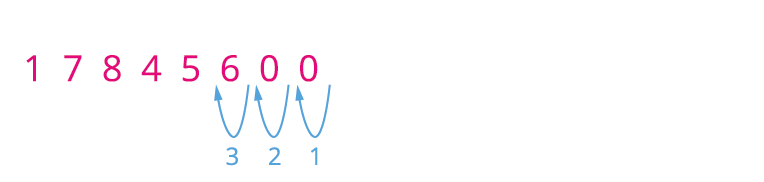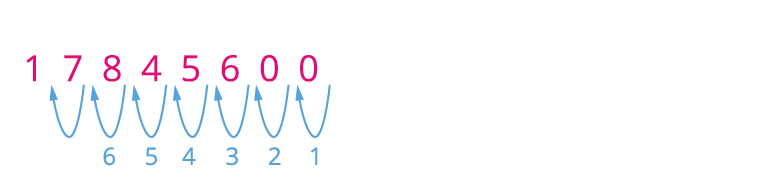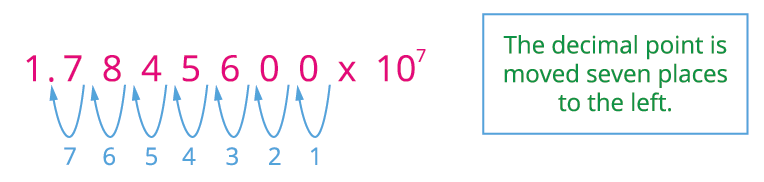
Now we'll learn how to convert the small numbers to standard form.
Converting small numbers to standard form:
When switching from a number to a normal notation (standard form) or vice versa, move the period to the right or left in the number and multiply it by \(10\) the appropriate degree.
If the number is less than \(1\), then writes it in the normal form \(10\) with a negative exponent.
If the given number is less than one, to convert that number to standard form, transfer the decimal to the right side of the number.
Example:
The mass of the smallest ants is approx. \(0.000001 kg =\) \(kg\).

Similarly, we can transform the following small number to standard form.
In the immediate next theory, we will learn step by step to convert the small number to standard form with some examples.