UPSKILL MATH PLUS
Learn Mathematics through our AI based learning portal with the support of our Academic Experts!
Learn moreLet us now see how we can write very small numbers in standard form.
We may use the following steps:
The small number to Standard form:
Step 1: Observe whether the number is between \(1\) and \(10\) or it is less than \(1\).
Step 2: If the number is between \(1\) and \(10\), then write it as the product of the number itself and .
Step 3: If the number is between \(0\) and \(1\), then move the decimal point to the right side so that there is just one digit on the left side of the decimal point.
Write the given number as the product of the number obtained and , here \(n\) denotes the number of places the decimal point has been moved to the right side.
However, the number obtained is the standard form of the given number.
The following examples will illustrate the above procedure.
Write the following numbers in standard forms.
i)
Step i) The given number is between \(0\) and \(1\).
Therefore to express in standard form, the decimal point is moved through only one place to the right so that there is just one digit on the left of the decimal point.
We are transforming the decimal point to one place to the right side of the given number so we can write this as .
Therefore we get .
ii) 0.000005.
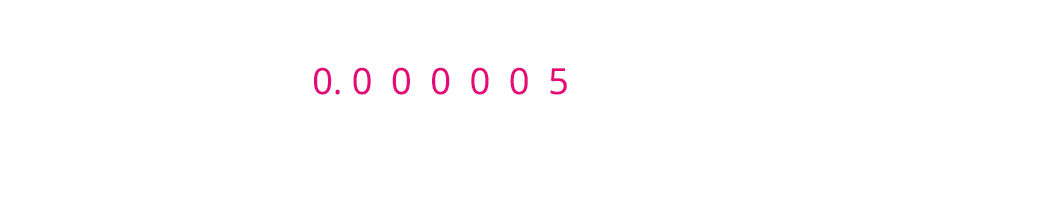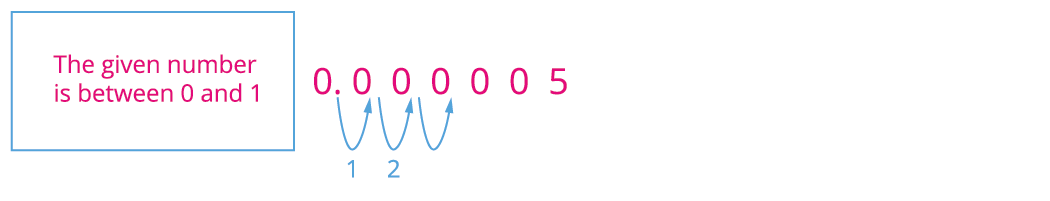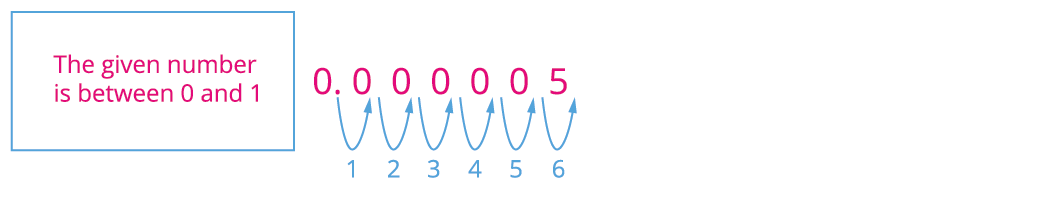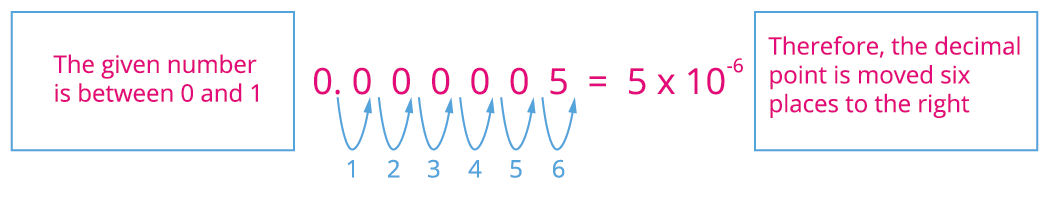
Similarly, for this number we have move the decimal point to six places to right side of the given number, which gives .
Therefore we get .
Register for free to see more content