PUMPA - SMART LEARNING
எங்கள் ஆசிரியர்களுடன் 1-ஆன்-1 ஆலோசனை நேரத்தைப் பெறுங்கள். டாப்பர் ஆவதற்கு நாங்கள் பயிற்சி அளிப்போம்
Book Free DemoA polygon is any shape with a minimum of three sides.
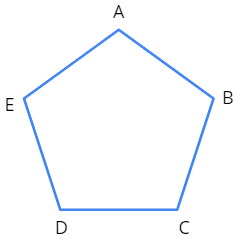
Let us consider the following pentagon \(ABCDE\) and try to find its area.
Area of a pentagon can be found in two ways.
Type \(1\)
Let us use the method of triangulation using two diagonals.
Let us look at the figure given below for a better understanding.
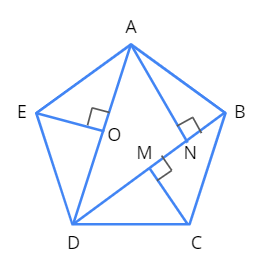
\(\text{Area of a pentagon} = \text{Area of}\) \(\triangle AED + \text{Area of}\) \(\triangle ABD + \text{Area of}\) \(\triangle BCD\)
Type \(2\)
Let us look at the figure given below for a better understanding.
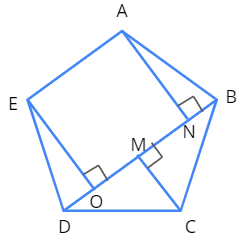
In the figure given above, \(BD\) is the diagonal, \(EO\) and \(AN\) are the two perpendiculars to \(BD\).
Here, \(\text{Area of a pentagon} = \text{Area of}\) \(\triangle ODE + \text{Area of}\) \(\triangle BCD + \text{Area of trapezium}\) \( AEON + \text{Area of}\) \(\triangle ABN\)
Register for free to see more content