PDF chapter test TRY NOW
A special quadrilateral is nothing but a rhombus. To find the area of a rhombus, we can use the same triangulation method as used in finding the area of a general quadrilateral.
A rhombus after triangulation is given below.
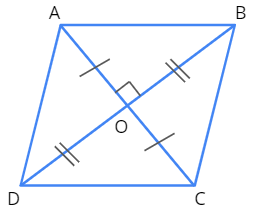
From the figure given above, we can come to the following inferences.
\(ABCD\) is a rhombus with diagonals \(AC\) and \(BD\).
Let \(AC\) be \(d_1\) and \(BD\) be \(d_2\). The diagonals \(d_1\) and \(d_2\) intersect at \(O\).
Also, as per the properties of a rhombus, the diagonals bisect each other.
\(\text{Area of the rhombus}\) \(ABCD =\) \((\text{Area of}\) \(\triangle ABD))\) \(+\) \((\text{Area of}\) \(\triangle BCD)\)
\(=\) \(\frac{1}{2} \times BD \times OA\) \(+\) \(\frac{1}{2} \times BD \times OC\)
\(=\) \(\frac{1}{2} \times BD \times (OA + OC)\)
\(=\) \(\frac{1}{2} \times BD \times AC\)
[Since \(AC = OA + OC\)]
\(=\) \(\frac{1}{2} \times d_1 \times d_2\)
[Since we have assumed that \(AC = d_1\), and \(BD = d_2\)]
Therefore, \(\text{area of a rhombus} = \frac{1}{2} \times d_1 \times d_2\) square units or the area of the rhombus is half the product of its diagonals.
Register for free to see more content