Area of a general quadrilateral — lesson. Mathematics CBSE, Class 8.

PDF chapter test TRY NOW

We know that a quadrilateral is made up of four sides. Any quadrilateral can be divided into two triangles with the help of a diagonal. This process of dividing a quadrilateral into triangles is called triangulation.

Let us look at the figure given below to know how a quadrilateral would look like after triangulation.

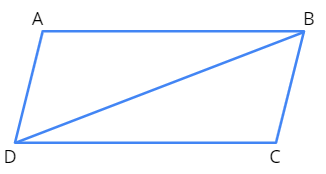
Here,

$\triangle ABD$ and

$\triangle BCD$ are formed after triangulation.

To find the area of the quadrilateral, we should know the values of

$h_1$ and

$h_2$ .

$h_1$ and

$h_2$ are the perpendiculars drawn from the diagonal to the vertices. Let us look at the figure given below for a better understanding.

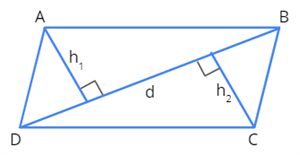
From the figure given above, we can come to the following inferences.

$ABCD$ is a quadrilateral with

$d$ as the diagonal and

$h_1$ and

$h_2$ as its heights.

$\text{Area of quadrilateral}$

$ABCD =$

$(\text{Area of} \triangle ABD)$

$+$

$(\text{Area of} \triangle BCD)$

[Since the diagonal is divided into two triangles after triangulation]

$=$

$(\frac{1}{2} \times BD \times h_1)$

$+$

$(\frac{1}{2} \times BD \times h_2)$

[Since,

$\text{Area of a triangle}= \frac{1}{2} \times b \times h$ ,where

$b$ and

$h$ are its base and height respectively]

$=$

$\frac{1}{2} \times BD \times (h_1 + h_2)$

$=$

$\frac{1}{2} \times d \times (h_1 + h_2)$

Therefore, $\text{Area of a quadrilateral}$

$=$

$\frac{1}{2}d(h1 + h2)$ square units.

Previous topic

Exit to the topic

Next theory

Send feedback

Did you find an error?

Send it to us!

1. Area of a general quadrilateral

Theory: